太極坐標是在極坐標的基礎上參考中國太極圖，將極徑用有向線段表示的新坐標。
解決了現有極坐標概念中極徑不能為負或者當作為因變數的極徑為負時卻將作為自變數的極角旋轉180°所帶來的諸多問題。
使用太極坐標能得到更統一的數學公式和更對稱的函式圖形。
使用太極坐標能重建數學秩序，諸如阿基米德螺線、玫瑰線等均可以納入數學主線，而不是被歸為“其它”的“重要曲線”。
使用太極坐標在極坐標中不存在的“六葉玫瑰線”等將得以存在。
基本介紹
- 中文名：太極坐標
定義,來源,太極坐標系,如何表示點,使用弧度單位,兩坐標系轉換,太極坐標方程,函式圖像,圖像對比,套用,意義,
定義
在平面內取一個定點O，叫極點，引一條射線Ox，叫做極軸，再選定一個長度單位和長度的正方向（通常取從極點向無窮遠方向）以及角度的正方向（通常取逆時針方向）。對於平面內任何一點M，用ρ表示有向線段OM的長度，用ρ'表示有向線段MO的長度（此時ρ'為負），θ表示從Ox到OM（或MO）的角度，ρ、ρ'叫做點M的極徑，θ叫做點M的極角，有序數對 (ρ,θ)、(ρ',θ)就叫點M的極坐標，這樣建立的坐標系叫做太極坐標系。
來源
第一個用極坐標來確定平面上點的位置的是牛頓。他的《流數法與無窮級數》，大約於1671年寫成，出版於1736年。此書包括解析幾何的許多套用，例如按方程描出曲線。書中創建之一，是引進新的坐標系。17甚至18世紀的人，一般只用一根坐標軸（x軸），其y值是沿著與x軸成直角或斜角的方向畫出的。牛頓所引進的坐標之一，是用一個固定點和通過此點的一條直線作標準，例如我們使用的極坐標系。牛頓還引進了雙極坐標，其中每點的位置決定於它到兩個固定點的距離。由於牛頓的這個工作直到1736年才為人們所發現，而瑞士數學家J.貝努利於1691年在《教師學報》上發表了一篇基本上是關於極坐標的文章，所以通常認為J.貝努利是極坐標的發現者。J.貝努利的學生J.赫爾曼在1729年不僅正式宣布了極坐標的普遍可用，而且自由地套用極坐標去研究曲線。他還給出了從直角坐標到極坐標的變換公式。確切地講，J.赫爾曼把cosθ,sinθ當作變數來使用，而且用n和m來表示cosθ和sinθ。歐拉擴充了極坐標的使用範圍，而且明確地使用三角函式的記號；歐拉那個時候的極坐標系實際上就是現代的極坐標系。
在極坐標中，x被ρcosθ代替，y被ρsinθ代替。ρ2=(x2+y2)
極坐標系是一個二維坐標系統。該坐標系統中的點由一個夾角和一段相對中心點——極點（相當於我們較為熟知的直角坐標系中的原點）的距離來表示。極坐標系的套用領域十分廣泛，包括數學、物理、工程、航海以及機器人領域。在兩點間的關係用夾角和距離很容易表示時，極坐標系便顯得尤為有用；而在平面直角坐標系中，這樣的關係就只能使用三角函式來表示。對於很多類型的曲線，極坐標方程是最簡單的表達形式，甚至對於某些曲線來說，只有極坐標方程能夠表示。
中國學者L在2006年用假設宇宙為3維超球面的模型研究類星體時，意識到用極坐標系來描述大尺度時空視界模型更方便，但同時發現現有極坐標系存在許多問題。後續受太極圖啟發，在2010年用類似添加負整數以擴充自然數系至整數系的方法，通過定義極徑為有向線段從而自然的擴充了極坐標系，並命名為“太極坐標系”。
太極坐標系
如何表示點
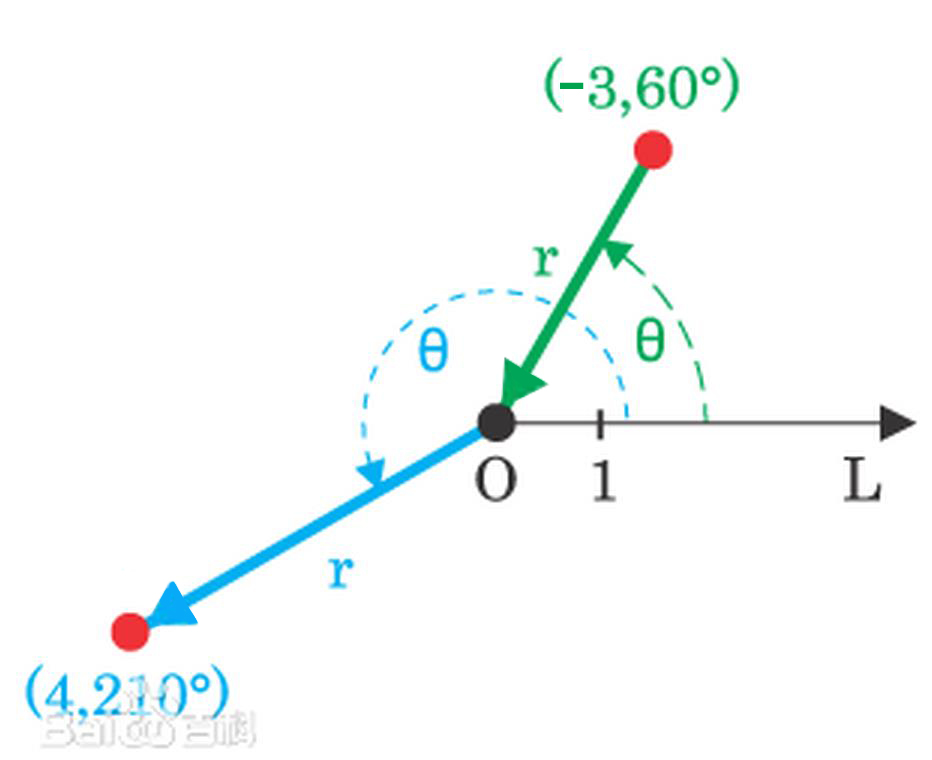
太極坐標正如所有的二維坐標系，太極坐標系也有兩個坐標軸：r（徑坐標）和θ（角坐標、極角或方位角，有時也表示為φ或t）。r坐標表示與極點的有向線段長度，θ坐標表示按逆時針方向坐標距離0°射線（極軸）的角度，極軸就是在平面直角坐標系中的x軸正方向。
比如，太極坐標系中的（3,60°）表示了一個以極點為起點且距離極點3個單位長度、和極軸夾角為60°的點。（−3,60°） 和（3,60°）表示了同一點，只是（−3,60°）所對應的有向線段以極點為終點。
太極坐標系中一個重要的特性是，平面直角坐標系中的任意一點，可以在太極坐標系中有無限種表達形式。通常來說，點（r，θ）可以任意表示為（r，θ ± 2kπ）但不能表示為（−r，θ ± (2k+ 1)π），這裡k是任意整數。如果某一點的r坐標為0，那么無論θ取何值，該點的位置都落在了極點上。
使用弧度單位
太極坐標系中的角度通常表示為角度或者弧度，使用公式2π rad = 360°.具體使用哪一種方式，基本都是由使用場合而定。航海（en:Navigation）方面經常使用角度來進行測量，而物理學的某些領域大量使用到了半徑和圓周的比來作運算，所以物理方面更傾向使用弧度。
兩坐標系轉換
太極坐標系中的兩個坐標r和θ可以由下面的公式轉換為直角坐標系下的坐標值
x = r*cos(θ)
y = r*sin(θ)
由上述二公式，可得到從直角坐標系中x和y兩坐標如何計算出太極坐標系下的坐標：
這裡尤其需要注意的是，在傳統極坐標系的定義下，r不含負號，所以極坐標與直角坐標間即使是在一個周期內也不能一一對應，只有考慮負號的太極坐標系才能建立起這種完整的對應關係。
太極坐標方程
用太極坐標系描述的曲線方程稱作太極坐標方程，通常用來表示ρ為自變數θ的函式。
太極坐標方程經常會表現出不同的對稱形式。如果ρ(−θ）= ρ（θ），則曲線關於極軸對稱。如果ρ（θ−α）= ρ（θ），則曲線相當於從極點逆時針方向旋轉α°。
函式圖像
為了更直觀的表示出極徑的取值，以下圖像均以偏紅色表示正（等價於極點為有向線段起點），偏藍色表示負（等價於極點為有向線段終點），具體對應關係見圖像右側色值對應條。
常函式r=k（圓）
右圖“圓”為函式 r=1(-π<θ<π) 的圖像
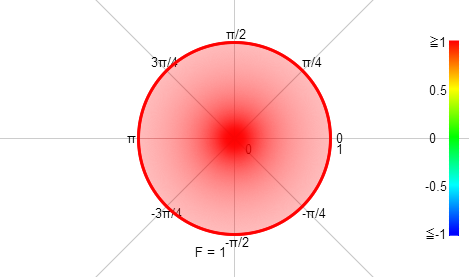圓
圓一次函式r=kθ+b（含阿基米德螺線）
右圖“心形線”為函式 r=θ(-π<θ<π) 的圖像
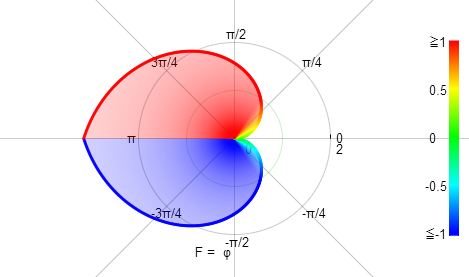心形線右圖“阿基米德螺線”為函式 r=θ(0<θ<2*π) 的圖像
阿基米德螺線三角函式（含直線、圓、玫瑰線）
太極坐標系尤其適合用於表示周期性函式，如三角函式。在太極坐標系下，一個新的卻又似曾相識的、聯繫的、對稱的、和諧的、統一的函式圖像世界躍然眼前！
1、正弦三角函式 r=a*sin(n*θ)（玫瑰線）
右圖“三角心形線”為函式 r=sin(0.5*θ) (-π<θ<π) 的圖像
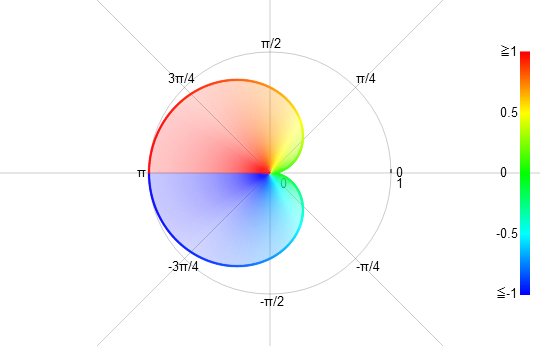三角心形線右圖“二葉玫瑰線”為函式 r=sin(1.0*θ) (-π<θ<π) 的圖像
事實上這是兩個圓，同時也是在傳統極坐標系下“不存在”的“二葉玫瑰線”
二葉玫瑰線右圖“三葉玫瑰線”為函式 r=sin(1.5*θ) (-π<θ<π) 的圖像
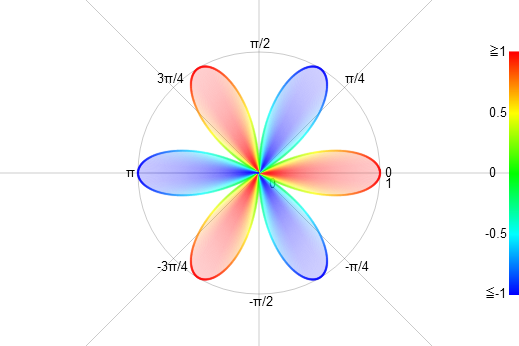
三葉玫瑰線右圖“四葉玫瑰線”為函式 r=sin(2*θ) (-π<θ<π) 的圖像
四葉玫瑰線右圖“五葉玫瑰線”為函式 r=sin(2.5*θ) (-π<θ<π) 的圖像
五葉玫瑰線右圖“六葉玫瑰線”為函式 r=sin(3.0*θ) (-π<θ<π) 的圖像
六葉玫瑰線是存在的，只是傳統極坐標系的定義有缺陷，就像自然數不包含負數一樣。
六葉玫瑰線
六葉玫瑰線上面羅列了六條正弦三角玫瑰線，是為了更直觀的顯示出玫瑰線的規律。
在太極坐標系下玫瑰線的葉數L與係數n之間的關係為L=2n（2n為自然數），這裡統一了在傳統極坐標系下n需要分奇偶數進行討論的各種情況，即使n為分數也成立。傳統極坐標系下不存在的二葉玫瑰線、六葉玫瑰線等曲線得以存在。同時也更自然的建立起了圓與玫瑰線之間的關係。
2、餘弦三角函式 r=a*cos(n*θ)（玫瑰線）
與正弦三角函式類似，只是作了90°旋轉，此處略
3、正切三角函式 r=a*tan(n*θ)（？線）
右圖“tan0.5”為函式 r=tan(0.5*θ) (-π<θ<π) 的圖像
tan0.5右圖“tan1.0”為函式 r=tan(1.0*θ) (-π<θ<π) 的圖像
tan1.0右圖“tan1.5”為函式 r=tan(1.5*θ) (-π<θ<π) 的圖像
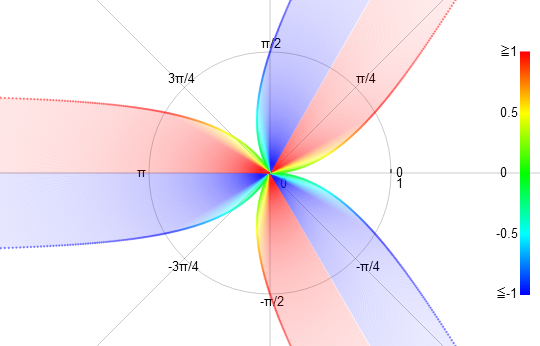tan1.54、餘切三角函式（？線） r=a*cot(n*θ)
與正切三角函式類似，只是作了90°旋轉，此處略
5、正割三角函式（？線） r=a*sec(n*θ)
右圖“sec0.5”為函式 r=sec(0.5*θ) (-π<θ<π) 的圖像
sec0.5右圖“sec1.0”為函式 r=sec(1.0*θ) (-π<θ<π) 的圖像
此時的函式圖像為一條直線，根據正割函式的定義，很容易證明。
sec1.0右圖“sec1.5”為函式 r=sec(1.5*θ) (-π<θ<π) 的圖像
sec1.56、餘割三角函式（？線） r=a*csc(n*θ)
與正割三角函式類似，只是作了90°旋轉，此處略。
進一步探討三角函式
接下來考慮分數情況,並將圖像繪製在同一張圖上，以便清晰的展現函式圖像隨參數變化的規律。
1、正弦三角函式 r=a*sin((n/m)*θ)
右圖“分數正弦”為函式 r=sin((n/m)*θ) (-π<θ<π) 的圖像
分數正弦2、餘弦三角函式 r=a*sin((n/m)*θ)
右圖“分數餘弦”為函式 r=cos((n/m)*θ) (-π<θ<π) 的圖像
分數餘弦3、正切三角函式 r=a*sin((n/m)*θ)
右圖“分數正切”為函式 r=tan((n/m)*θ) (-π<θ<π) 的圖像
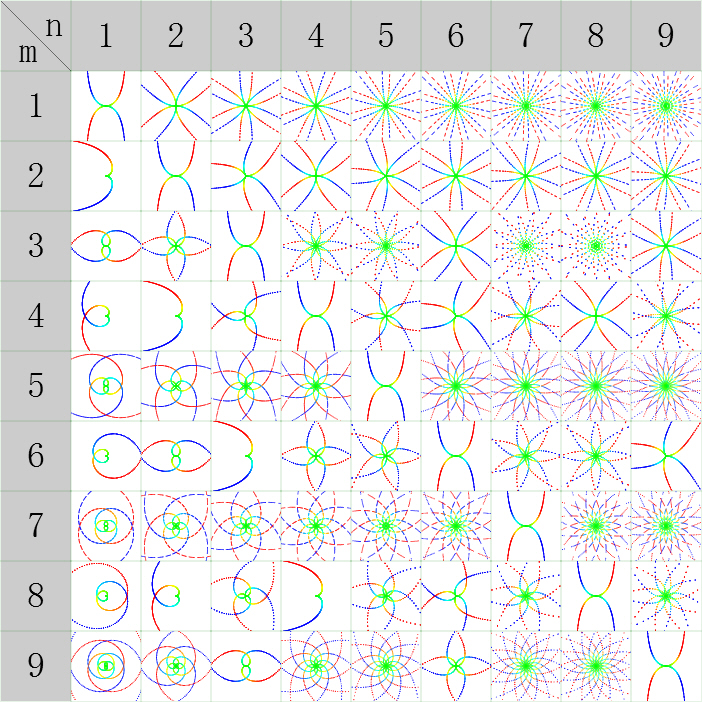分數正切4、餘切三角函式 r=a*cot((n/m)*θ)
右圖“分數餘切”為函式 r=cot((n/m)*θ) (-π<θ<π) 的圖像
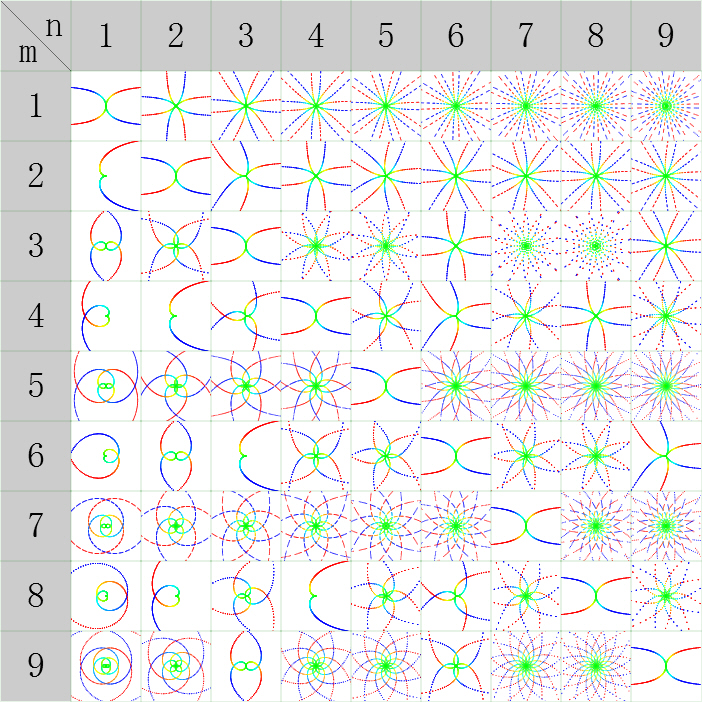分數餘切5、正割三角函式 r=a*sec((n/m)*θ)
右圖“分數正割”為函式 r=sec((n/m)*θ) (-π<θ<π) 的圖像
6、餘割三角函式 r=a*csc((n/m)*θ)
右圖“分數餘割”為函式 r=csc((n/m)*θ) (-π<θ<π) 的圖像
分數正割
分數餘割三角函式合集
右圖“三角函式合集”為以上六種三角函式圖像的疊加，在此不得不驚嘆三角函式的對稱！數學的自然之美！若是要用一句話來形容。我唯一想到的是：
“那難道不是出自上帝之手嗎？”
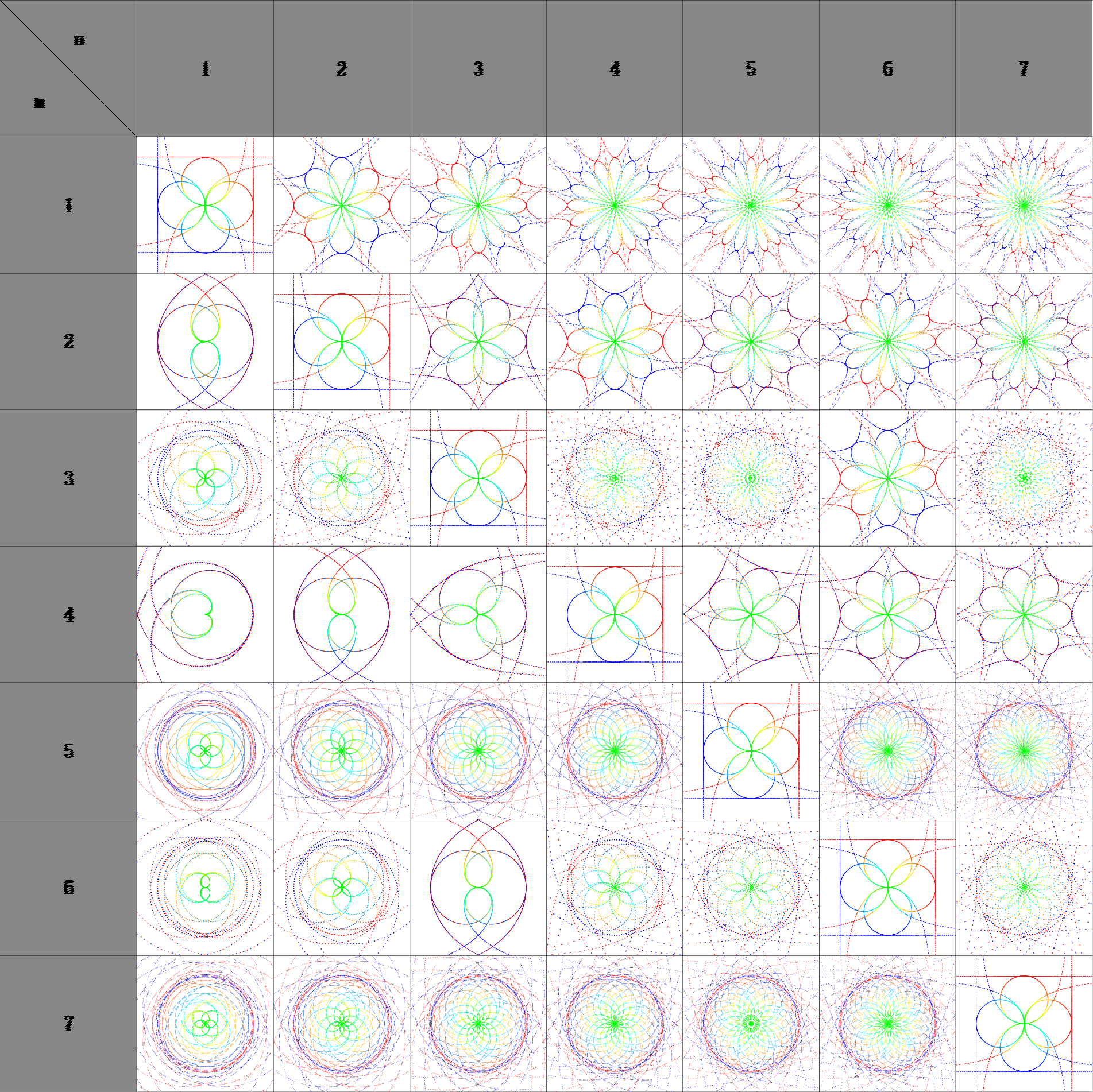三角函式合集對數函式
右圖“對數函式”為函式 r=ln(θ) (-π<θ<π) 的圖像
對數函式更多函式圖像，略。
圖像對比
右圖“函式及其圖像”為常見初等函式在不同坐標系中的圖像對比。
函式及其圖像
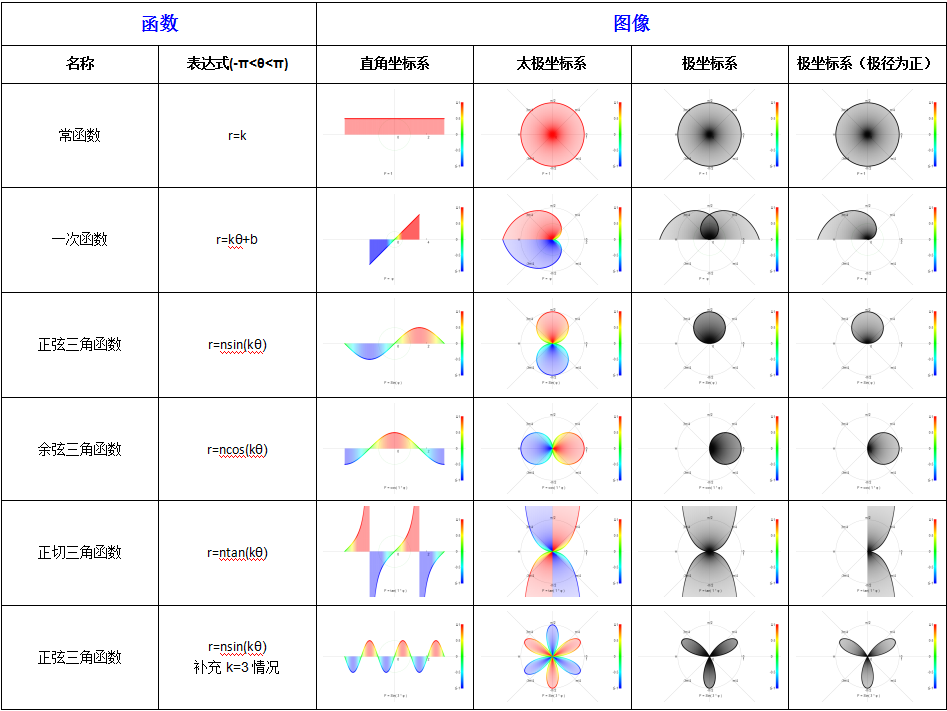函式及其圖像包括笛卡爾直角坐標系、太極坐標系、極坐標系、極坐標系（當規定極徑為不能為負的情況，可命名為半極坐標系）
在k=3的正弦函式中能夠最明顯的看到傳統極坐標系的殘缺。事實上，此時的極坐標系即使在一個周期內且允許極逕取負值，也沒能建立起與直角坐標系間的一一對應關係，是不完備的。這極大限制了極坐標系的套用。
傳統極坐標系中的函式圖像由於當因變數為負時改變自變數，導致一個周期內同一自變數對應兩個因變數。若要更準確的表示出這種改變在笛卡爾直角坐標系中的對應關係，以k=3的正弦函式為例，見右圖“三種極坐標對應的直角坐標”所示。
如果說傳統極坐標也允許極徑為負，那么它的問題的關鍵就在於不應該通過改變作為自變數的極角來處理這種情況。這是導致諸多不對稱、不統一的根源。
三種極坐標對應的直角坐標
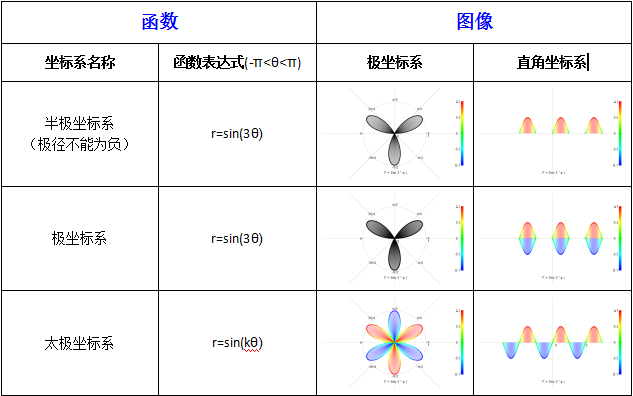三種極坐標對應的直角坐標套用
行星運動的克卜勒定律：
克卜勒第二定律：太極坐標提供了一個表達克卜勒行星運行定律的自然數的方法。克卜勒第一定律，認為環繞一顆恆星運行的行星軌道形成了一個橢圓，這個橢圓的一個焦點在質心上。上面所給出的二次曲線部分的等式可用於表達這個橢圓。克卜勒第二定律，即等域定律，認為連線行星和它所環繞的恆星的線在等時間間隔所劃出的區域是面積相等的，即ΔA/Δt是常量。這些等式可由牛頓運動定律推得。
意義
太極坐標系啟示我們可以用一種更統一的方式重新建立數學知識的結構。
在講函式及其圖像的時候可以同時考慮笛卡爾直角坐標系、極坐標系(甚至可以區分含與不含負極徑兩種情況)、太極坐標系等。這樣可以更直接的建立知識間的聯繫，將零星散亂的“其他”已知或未知的“重要曲線”納入到一個統一的框架中。
現有的數學教材與工具書均應該用這種方式重寫。
