基本介紹
- 書名:多焦點圓
- 定價:10.0
基本信息,定義,特徵特性,類型,作圖,分析方法,參數分析,特徵參數分析,
基本信息
多焦點圓是泛指不同焦點數和不同焦點形狀,符合一定規則形成的凸閉合曲線圖形的總稱,是圓和橢圓概念的擴展。

定義
為.便於對多焦點圓、橢圓和圓的統一描述,引用相關術語。(1)定點:平面內的已知點或固定點。(2)焦點環線:環繞定點一周最短的環形線,用L0表示。(3)焦點多邊形:焦點環線形成的幾何圖形。(4)焦點:焦點多邊形頂點的定點。(5)環線:動點與焦點多邊形所形成的環形線,用L表示。
有了圖1和術語,可以對多焦點圓作初步的描述,把多焦點圓看作是以焦點多邊形為“圓心”,環線為“半徑”的“圓”。
多焦點圓定義:平面內,與n(n>0的整數)個定點間形成的環線長為常數的點的軌跡稱做多焦點圓。定點間的環線形狀稱做焦點多邊形,頂點稱做焦點,焦點多邊形是多焦點圓的基本屬性。
特徵特性
環線比值(k )
環線長和焦點環線長的比值K為無單位量,是多焦點圓的形狀特徵和屬性的參數。表達式為:
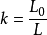
環線長比值(k )在對稱多焦點圓的圖形與參數和特徵參數分析中,起到重要作用。
多焦點圓的曲線
圓周曲線是由環線和焦點所確定的多條不同的橢圓曲線,通過相切連線形成的凸閉合光滑曲線。選擇適合的坐標系,各段橢圓曲線根據參數均可建立對應的橢圓方程,能夠對圖形作具體分析。
多焦點圓的圖形
多焦點圓是有規則的凸閉合曲線圖形。環線、焦點數目和形狀是多焦點圓的基本參數,確定多焦點圓的圖形特徵如:圖形的大、小;形狀的長、扁和對稱性等。焦點多邊形具有形和量的變化特徵,參數的任何一項變化,都會引起圖形的相應變化,屬於多參數圖形。
類型
儘管多焦點圓有多種不同的形狀,根據圖形特徵,分為對稱和非對稱兩類。
對稱多焦點圓
焦點多邊形為對稱幾何圖形的多焦點圓稱為對稱多焦點圓。對稱多焦點圓具有對稱軸,根據對稱軸數目進一步分為:
一條對稱軸多焦點圓——卵形曲線
焦點多邊形為等腰三角形、紡錘形(一條對角線為對稱軸,對稱邊相等的四邊形)、等腰梯形和其他具有一條對稱軸圖形的多焦點圓,圖形類似家禽和鳥類卵的形狀,稱為卵形曲線。規範的卵形曲線稱為普通卵圓;具有形成圖形內在規律的規範卵形曲線稱為標準卵圓。根據焦點形狀和數目命名。
兩條對稱軸多焦點圓——橢圓形曲線
焦點多邊形為線形、棱形、長方形、六邊形等具有兩條對稱軸圖形的多焦點圓稱為橢圓形曲線。規範的橢圓形曲線稱為普通橢圓,具有形成圖形內在規律的橢圓稱為標準橢圓,根據焦點形狀和數目命名。
三條及其以上對稱軸多焦點圓——多軸圓
焦點為正多邊形的多焦點圓有多條對稱軸,對稱軸數與焦點正多邊形的邊數相同;重心在中點,類似於圓的圓心,屬於規範標準曲線圖形,故稱為多軸圓,根據正多邊形命名。
非對稱多焦點圓
焦點多邊形為非對稱幾何圖形的多焦點圓,稱為非對稱多焦點圓。如焦點為任意三角形、任意四邊形以及其他沒有對稱軸多邊形的多焦點圓。非對稱性多焦點圓圖形複雜,沒有確定的外部特徵,大部分多焦點圓屬於這一類。
對稱多焦點圓具有獨特的外部特徵——長、寬和半軸(寬與對稱軸交點將對稱軸分為上、下不相等的半軸,長的半軸簡稱為半軸下同),外部特徵值稱為特徵參數。為了方便敘述,把對稱多焦點圓簡稱為多焦點圓(下同)。
作圖
根據多焦點圓定義,介紹一種簡易的針線作圖方法:(1)自製能縮、放的環形線、大頭針、直尺和筆。(2)在作圖平面上作出已知點或多邊形。(3)將大頭針分別直立、固定在已知點或多邊形的頂點上;(4)將符合長度的環形線套在大頭針外,畫筆由內向外拉直環線移動一周。
針線作圖屬於連續移動的基本作圖方法,適合圓和橢圓的作圖和施工放樣,作圖軟體有待開發。
分析方法
多焦點圓的環線(L)和焦點多邊形的參數稱為參數;反映圖形特徵的長、寬和半軸稱為特徵參數。可以從參數和特徵參數兩方面,分析多焦點圓的圖形特徵。
參數分析
根據已知參數值,建立參數與特徵參數關係式,對多焦點圓作以下幾方面分析:(1)計算對稱多焦點圓的特徵參數(長、寬、和半軸)。(2)計算周長(近似值)、面積。(3)建立各弧段的橢圓方程。(4)多焦點圓作圖。(只有參數方可作圖)。(5)多焦點圓的圖形設計。
特徵參數分析
根據對稱多焦點圓的特徵參數求解參數,再由所求的參數對多焦點圓作參數分析。由於多焦點圓的參數與特徵參數關係的複雜性,難以直接解出參數值。通過建立多焦點圓的參數與特徵參數關係式,採用參數模擬計算方法,能夠對四個焦點以內的對稱多焦點圓的參數求解。

