基本列(fundamental sequence)亦稱柯西列，是極限存在的數列，也就是滿足柯西條件的數列，即這樣的{xn}：對任意正整數ε，存在正整數N，使當n，m>N時，有|xn-xm|<ε，反映在數軸上，表示當項的編號無限增加時，基本列中任意兩項之間的距離將會任意地小，不難想像這種點列中的點最終將聚集在某個點的周圍，即收斂於這個點，反之，如果一個點列收斂，編號無限增大的項之間的距離也將任意地小，這就是說：實數列收斂，若且唯若它是基本列，這個結論稱為柯西準則。若一個基本列的所有各項都是有理數，則它為基本有理數列，但基本有理數列不一定收斂於有理數。例如，設en=1+∑nk=1(1/(k!))，則{en}∞n=1是基本有理數列，但它的極限e是無理數。康托爾(G.F.P.Cantor)注意到基本有理數列與基本實數列之間的這個差別，利用基本有理數列定義實數.康托爾的實數定義，是多種互相等價的實數定義中的一種，主要反映了實數的完備性。基本列的概念可以推廣到Rn及一般的抽象空間，並用以使這些空間完備化。
基本介紹
- 中文名：基本列
- 外文名：fundamental sequence
- 別稱：柯西列，Cauchy列
- 所屬學科：數學（數學分析）
- 簡介：極限存在的數列
基本概念,相關性質定理,
基本概念
設{an}是一實數列，對任意給定的ε>0，若存在N∈N*，使得當m,n∈N*且m,n>N時，有
粗略地說，基本列的特徵是:只要數列中兩個項充分地靠後，而不論它們的相對位置如何，它們之差的絕對值便可以小到事先任意給定的程度。
在定義中，顯然只需考慮m>n的情形。我們可以令m=n+p，這樣一來，基本列的定義可以等價地敘述為：對任意給定的ε>0，若存在N∈N*，使得當n>N時，
相關性質定理
下面中心的議題是要證明：一個數列是收斂數列的充分必要條件是，它是基本列。為此，我們需做一些預備工作。
引理1 從任一數列中必可取出一個單調子列。
證明 先引人一個定義：如果數列中的一項大於這個項之後的所有各項，則稱這一項是一個“龍頭”。分兩種情況來討論.
情況(a)如果在數列中存在著無窮多個“龍頭”,那么把這些可作“龍頭”的項依次取下來，顯然將得到一個嚴格遞減的數列.
情況(b) 設在此數列中只有有限多個項可作“龍頭”.這時取出最後一個“龍頭”的下一項,記作
.由於不是“龍頭”,在它的後邊必有一項
(i2>i1)滿足≤;因也不是“龍頭”,在它的後邊也必可找到一項
(i3>i2),使得≥.如此進行下去,就得到子列{
},它顯然是一個遞增的子列。
定理1(列緊性定理) 從任何有界的數列中必可選出一一個收斂的子列。
此定理也稱作Bolzano(波爾查諾,1781~1848)- Weierstrass(魏爾斯特拉斯，1815~1897)定理。
證明 設{an}是一個有界的數列.根據引理1，從中可以取出一個單調子列{}，這個子列當然也是有界的。易知{}是一個收斂數列。
現在來證明本節的主要定理。
定理2 一個數列收斂的充分必要條件是，它是基本列。
證明 必要性。設{an}是一個收斂數列，其極限記作a。因此，對任意給定的ε>0，存在正整數N,當n>N時,有
充分性。設{an}是一個基本列，首先證明基本列必是有界的，對ε0=1而言,可以取出一個N∈N*,且當n>N時,有
根據定理1，從有界數列{an}中可選出一個收斂的子列{}，設→a (n→∞)。我們來證明這個a也是數列{an}的極限。由於{an}是基本列，對任給的ε>0,存在一個N1∈N*,使得當m，n>N1時，都有
又因
,對任給的ε>0,存在N2∈N*,當k>N2時，
現取N= max(N1,N2),當n>N時，有
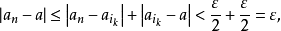
定理2又稱為數列的Cauchy收斂原理，是一個在理論上非常重要的定理，在數學分析的全部內容中，有著各式各樣的表述，它告訴我們，當我們來判斷一個數列是否收斂時，只需通過數列的自身，而無須求助於另外的數，還應指出的是，Bolzano- Weierstrass定理和Cauchy收斂原理是實數系統連續性的另外兩種表現形式。
