基本介紹
- 中文名:基數加法
- 外文名:addition of cardinal numbers
- 所屬學科:數學
- 簡介:定義在基數類上的二元運算
基本介紹
基數加法的性質






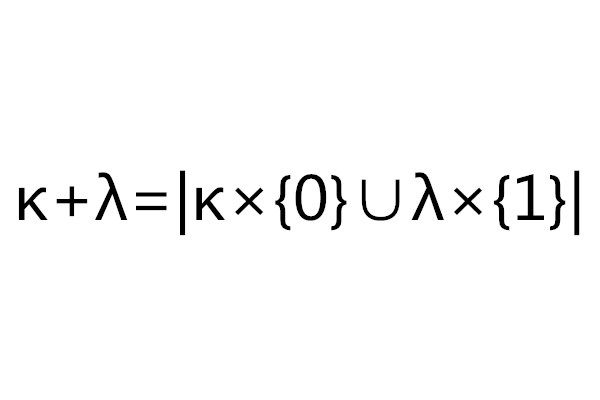






基數加法(addition of cardinal numbers)是自然數加法的超窮推廣,是定義在基數類上的二元運算。兩個基數κ與λ的和,指將κ的元素與λ的元素合併起來構成的集合的基數,即κ+λ=|κ×{0}∪λ×{1...
基數加法 兩個基數κ與λ的和,指將κ的元素與λ的元素合併起來構成的集合的基數,即κ+λ=|κ×{0}∪λ×{1}|。基數的加法運算滿足交換律與結合律。基數的加法運算還可以擴充到無窮多個基數的加法運算.設〈κ:i∈I〉為一個基數序列,I為指標集,定義 式中κ表示〈κ:i∈I〉的廣義笛卡兒n乘積。基數...
基數指數是|X|^|Y| = |X^Y|,其中 X^Y 是所有由 Y 到 X 的函式的集合。普通性質 在有限集時,這些運算與自然數無異。一般地,它們亦有普通算術運算的特質:加法和乘法是可交換的,即 |X|+|Y|=|Y|+|X| 及 |X||Y|=|Y||X|。加法和乘法符合結合律,(|X|+|Y|)+|Z|=|X|+(|Y|+|Z|...
矩陣加法:為相同大小的兩個矩陣定義矩陣加法。 由A + B表示的兩個m×n(發音為“m乘n”)的矩陣A和B的和是通過相加元素而計算的矩陣,例如:集合理論和類別理論中的加法 增加自然數的方法是在集合理論中添加序數和基數。這些給出了兩個不同的概括,即自然數。與大多數加法操作不同,序數的加法是不可交換的...
加法:T+T=T1,T+0=T,T+1=0,0+T=T,0+0=0,0+1=1,1+T=0,1+0=1,1+1=1T 1+11=1TT,1+111=1TTT,1+1111=1TTTT,1+11111=1TTTTT,1+111111=1TTTTTT T+TT=T11,T+TTT=T111,T+TTTT=T1111,T+TTTTT=T11111,T+TTTTTT=T111111 連續多個1和1相加,等於將加數1移至被加數連續...
弱不可達基數是一種正則基數。既是極限基數又是正則基數的不可數基數。若 為弱不可達基數,則 ,且α是極限序數。因為 ,所以 。可見 是非常大的。由定義還可看出,不可達基數κ不可能由比它小的基數通過基數的加法、乘法、乘冪和取極限等運算得到。豪斯多夫(F.Hausdorff)在1908年提出了弱不可達基數的概念。現...
進位就算是在高等數學中也是會出現的。 在計算中,進位是加法器電路的重要功能。以個位向十位進位為例:基數為10(2進制的基數是2,類推),個位這個數位上的數量達到了10的情況下,則個位向前一位進1,成為一個十。在十進制的算法中,個位滿十,在十位中加1;十位滿十,在百位中加一。在二進制的算法中,...
加法 + TT T0 T1 T 0 1 1T 10 11 11 0 1 1T 10 11 1TT 1T0 1T1 10T 10 T 0 1 1T 10 11 1TT 1T0 - 1T T1 T 0 1 1T 10 11 - - 1 T0 T1 T 0 1 1T - - - 0 TT T0 T1 T 0 1 - - - T T11 TT T0 T1 T 0 - - - T1 T10 T11 TT - - - - - - T0 T1T ...
二進制(binary),是在數學和數字電路中以2為基數的記數系統,是以2為基數代表系統的二進位制。這一系統中,通常用兩個不同的符號0(代表零)和1(代表一)來表示。發現者是萊布尼茨。數字電子電路中,邏輯門的實現直接套用了二進制,現代的計算機和依賴計算機的設備里都使用二進制。每個數字稱為一個比特(Bit,...
進位制/位置計數法是一種記數方式,故亦稱進位記數法/位值計數法,可以用有限的數字元號代表所有的數值。可使用數字元號的數目稱為基數(en:radix)或底數,基數為n,即可稱n進位制,簡稱n進制。現在最常用的是十進制,通常使用10個阿拉伯數字0-9進行記數。對於任何一個數,我們可以用不同的進位制來表示。比如...
只有0和1兩個數碼,基數為二。 加法 如下: (1)首先是最右數碼位相加。這裡加數和被加數的最後一位分別為“0”和“1”,根據加法原則可以知道,相加後為“1”。 (2)再進行倒數第二位相加。這裡加數和被加數的倒數第二位都為“1”,根據加法原則可以知道,相加後為“(10)2”,此時把後面的“0”留下,而把第一...
一個十進制數由一個基數序列組成,每一位數字的命名取決於其相對於小數點的位置。例如:507.36表示5個100(10),加0個10(10),加7個最小整數單位1(10),加3個0.1(10),加6個0.01(10)。該計數法的一個要點(也是其實現的難點)是對0與其它基數一視同仁。算術運算 算術運算指加法、減法、乘法...
經過快心算的訓練,學前孩子可以深刻的理解數學的本質(包含),數的意義(基數,序數,和包含),數的運算機理(同數位的數的加減,)數學邏輯運算的方式,使孩子掌握處理複雜信息分解方法,發散思維,逆向思維得到了發展。孩子得到一個反應敏銳的大腦。存疑:從1加到100速算得到5050的故事有抄襲高斯速算的嫌疑,幾乎...
(1)二進制轉換成十進制:基數乘以權,然後相加,簡化運算時可以把數位數是0的項不寫出來,(因為0乘以其他不為0的數都是0)。小數部分也一樣,但精確度較少。(2)二進制轉換為八進制:採用“三位一併法”(是以小數點為中心向左右兩邊以每三位分組,不足的補上0)這樣就可以輕鬆的進行轉換。例:將二...
二十四進制有24個基數:0、1、2、3、4、5、6、7、8、9、A(10)、B(11)、C(12)、D(13)、E(14)、F(15)、G(16)、H(17)、J(18)、K(19)、L(20)、M(21)、N(22)、P(23)(A~~P代表10~~23)。為了避免混淆1和I,0和O,故跳過字母I、O,18~~23分別計作J、K、L...
七進制是以7為基數的記數系統,使用的數碼為0、1、2、3、4、5、6。表示 七進制小數通常都是循環小數,除非分母是七的倍數。有些小數可以用有限個數字來表示:乘除加減法表 七進制的乘法表:七進制的除法表:七進制的加法表:七進制的減法表:在七進制中: π = 3.0663651432... e = 2.5012410654...加法...
Ⅲ.基數‘三’的諷識及中央和上下四方的辨別 Ⅳ.基數‘一’‘二’‘三’的複習 三、三角形 Ⅰ.三角形的認識 四、基數‘四’‘五’Ⅰ.基數‘四’的認識 Ⅱ.基數五的認識 Ⅲ.基數‘一’到‘五’的複習 五、基數‘六’‘七’和星期 Ⅰ.基數‘六’的認識 Ⅱ.和數為六的加法 Ⅲ.基數‘七’的...
