坐標表象

坐標表象指選取代表位型空間的完備基矢，來描述物理態對應的矢量、可觀測量對應的算符以及物理學規律所對應的方程的一種表示方法（直白而不嚴格地說就大概就是用波函式來描述量子物理學問題的方法）。

基本介紹

• 中文名：坐標表象
• 外文名：coordinate representation 

定義

每個物理態對應一個右矢量空間中的右矢量，而這些右矢量可以用不同的完備基進行展開：

而我們同樣可以選取代表坐標表象的完備基，然後將一個物理態表述到位型空間(注意：本節以及下一小節都選取的是一維位型空間，但做類似的簡單推廣就可以得到多維位型空間的結果)：

其中A為一個歸一化係數，不妨設為1。

我們稱為該物理態的右矢量在坐標表象中的表示。類似的，左矢量可以表示為，算符表示為。

一般而言，就是波函式，而對應波函式的復共軛。而一般對應為微分算符。

性質

對於一般性態矢量空間所滿足的方程，都可以通過插入：

進行改寫，之後再利用歸一化條件：

把冗餘的參量積分掉，就可以得到物理規律在坐標表象對應的方程。

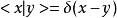
此外，動量表象下的物理規律與坐標表象只差一個傅立葉變換。

套用

坐標表象是所有表象中最常用的之一，這是因為我們所有的測量都是在位型空間中進行，故而用波函式（也就是坐標表象）來描述空間機率分布就顯得與實驗直接相關。

一般而言，比較低能的凝聚態物理、原子分子物理等領域中跟空間分布關聯較大的問題會更多的套用坐標表象進行分析。而由於求解偏微分方程的複雜性，也由於不是所有物理態都可以用解析波函式來表示，使得坐標表象的套用受到一定程度的限制。