圓內整點問題(lattice point in circle problem) 數論中的著名問題.用r(n)表示將非負整數n分解成兩個平方數之和的分法種數.和數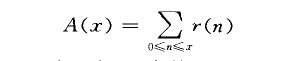
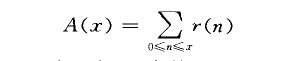
就等於落在圓u2-}v2鎮x內的整點(u,v)(即u,v均為整數的點)的個數.圓內整點問題就是去尋求最小的B,使A(x)=}r(x)+D(xB+E)對所有。>0都成立.高斯(Gauss , C. F.)首先證明了
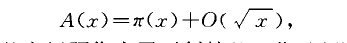
為圓內整點問題作出了開創性的工作,因此圓內整點問題也稱高斯圓問題.
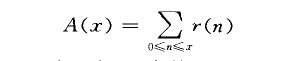
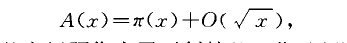
圓內整點問題(lattice point in circle problem) 數論中的著名問題.用r(n)表示將非負整數n分解成兩個平方數之和的分法種數.和數 就等於落在圓u2-}v2鎮x...
廣義圓內整點問題(Generalized cirele latticepoint in circle problem)數論中的重要問題.研究n維橢球 中的整點個數A(.W -A},Cx),其中FCu‑ua,...}u‑...
格點,又稱整點,指坐標都是整數的點,格點問題就是研究一些特殊區域甚至一般區域中的格點的個數的問題。...
《數論經典著作系列:解析數論基礎(第2版)》以解析數論的四個著名問題:平面區域內的整點問題、素數分布問題、Goldbach問題和Waring問題為中心,很好地闡明了解析數論的...
