基本介紹
- 中文名:圍坐問題
- 外文名:menage problem
- 提出者:盧卡斯
- 提出時間:1891年
- 適用領域:組合數學
- 套用學科:數學
具體表述
問題意義
圖夏爾等式

證明過程























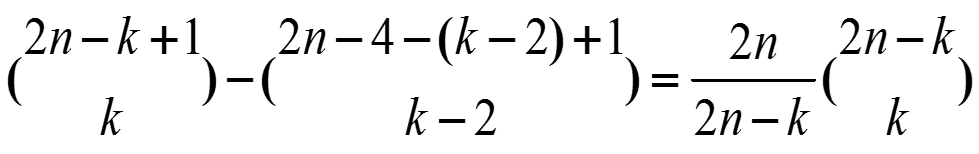
理論解釋

























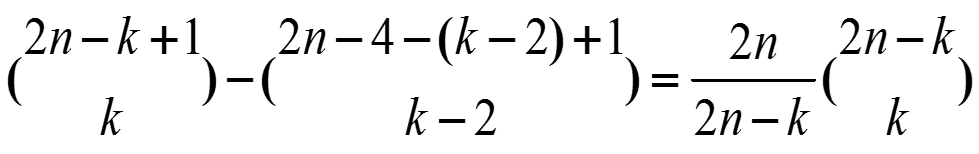

圍坐問題的的原型是N對夫妻圍坐問題。這個問題由盧卡斯(Édouard Lucas)在1891年首先提出來,直到1934年圖夏爾才給出一個具體表達式,但是未給出具體證明。這個問題與扭結理論,圖理論等有著密切關係。圍坐問題(...
夫妻對入座問題又叫Menage問題、夫妻問題(problem of mate),是一種圓排列問題,呂卡(F.-É.-A.Lucas)於1891年提出的一個趣味組合問題,有n個丈夫和他們的妻子圍坐在一張圓桌旁,要使男女依次交錯入坐,且使沒有一個妻子坐在她...
圍坐 圍坐,漢語詞語,拼音是wéi zuò,意思是圍成一圈而坐。解釋 圍成一圈而坐。出處 例如:小時候,大家最喜歡圍坐在老樹下,聽阿公講古。
這個問題可以用來解釋死鎖和資源耗盡。問題描述 哲學家就餐問題可以這樣表述,假設有五位哲學家圍坐在一張圓形餐桌旁,做以下兩件事情之一:吃飯,或者思考。吃東西的時候,他們就停止思考,思考的時候也停止吃東西。餐桌中間有一大碗義大利...
附錄A如何確定你的核心故事 199 附錄B對你自己的故事講述情況的評估表 203 附錄C公司故事模板 207 故事題目 209 挑戰 210 解決問題的方法 210 解決方案 21l 結果/回報 211 構造故事 211 附錄D關於關鍵性的工作場所學習的研究 213 ...
附錄A如何確定你的核心故事 199 附錄B對你自己的故事講述情況的評估表 203 附錄C公司故事模板 207 故事題目 209 挑戰 210 解決問題的方法 210 解決方案 21l 結果/回報 211 構造故事 211 附錄D關於關鍵性的工作場所學習的研究 213 ...
114.三十六軍官問題 115.夫妻圍坐問題 116.柯克曼女生問題 十二、分割趣題 117.分割正方形 118.小墊面料 119.分花 120.切豆腐 121.免嫉妒分割 十三、漢字推理題目 122.筆畫考察 123.封閉區域考察(1)124.封閉區域考察(2...
各方當事關聯人和心理疏導師圍坐玻璃屋四周,以燈光變換喻示任何問題都是“多維”的,你必須通盤考慮、全景梳理,才不會有所忽略,從而找到“幸福之門”。對於這個舞台設計,製片人陳曄毫不隱瞞靈感來自《Lie to me》,“不過沒想到把...
在第一次召開草圖觀摩工作會時,黨史專家描述了延安哲學小組成立的情景,我覺得很有道理,更加貼近這次紀念活動的主題,豐富了這幅畫背後的故事,所以,我查看了許多有關延安革命方面的資料,意外發現當時圍坐在毛澤東身邊研究哲學問題的...
