在非線性動力學等非平衡態體系中,環境的隨機擾動在相空間內呈現非均分布,其同相分量漲落被壓縮,正交分量漲落膨脹。該效應被稱為擠壓效應。
基本介紹
- 中文名:噪聲擠壓效應
- 外文名:squeezing effect
noise squeezing - 適用領域:非線性動力學,光學,量子,通信,感測
- 所屬學科:物理+數學
定義
性質
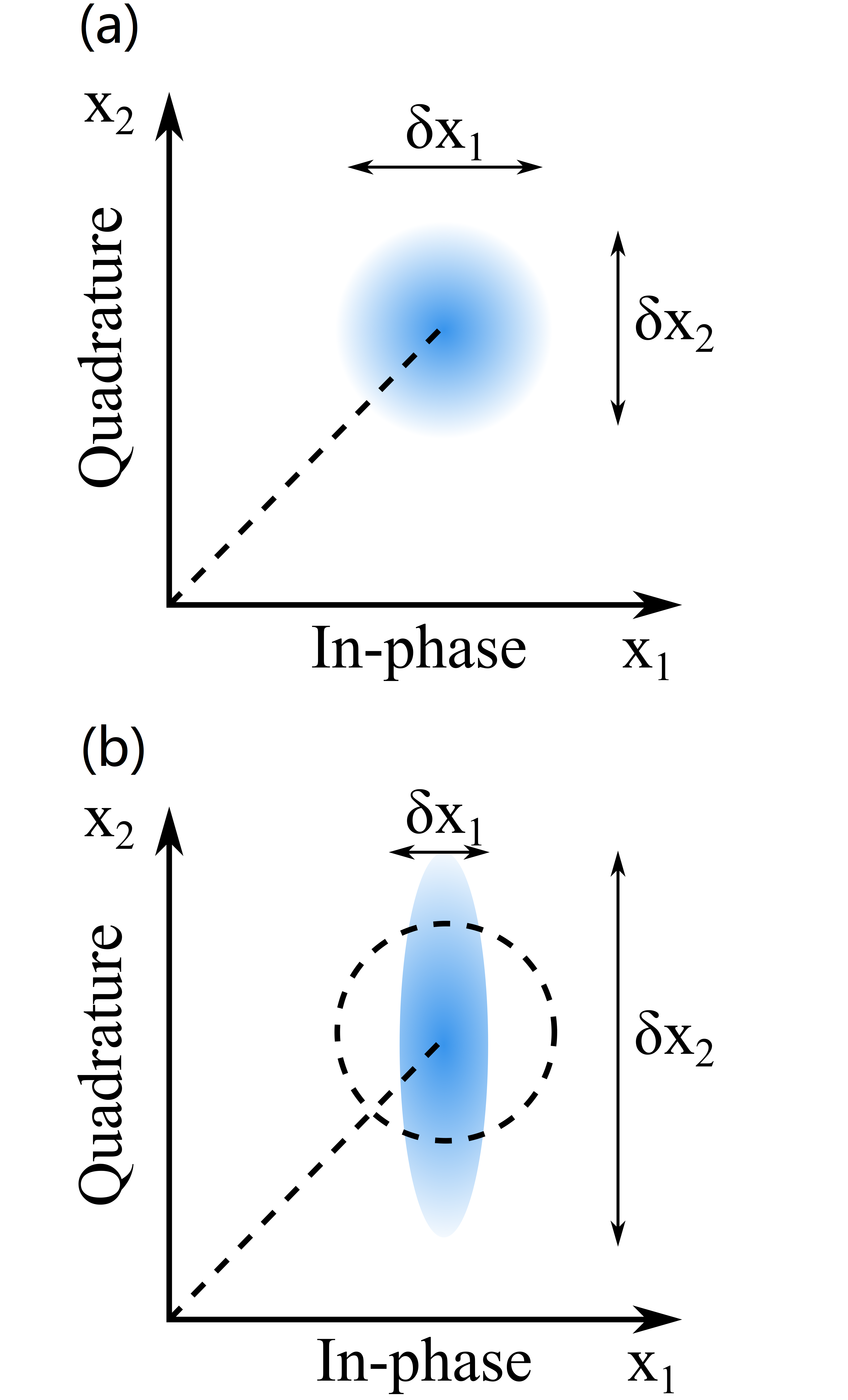



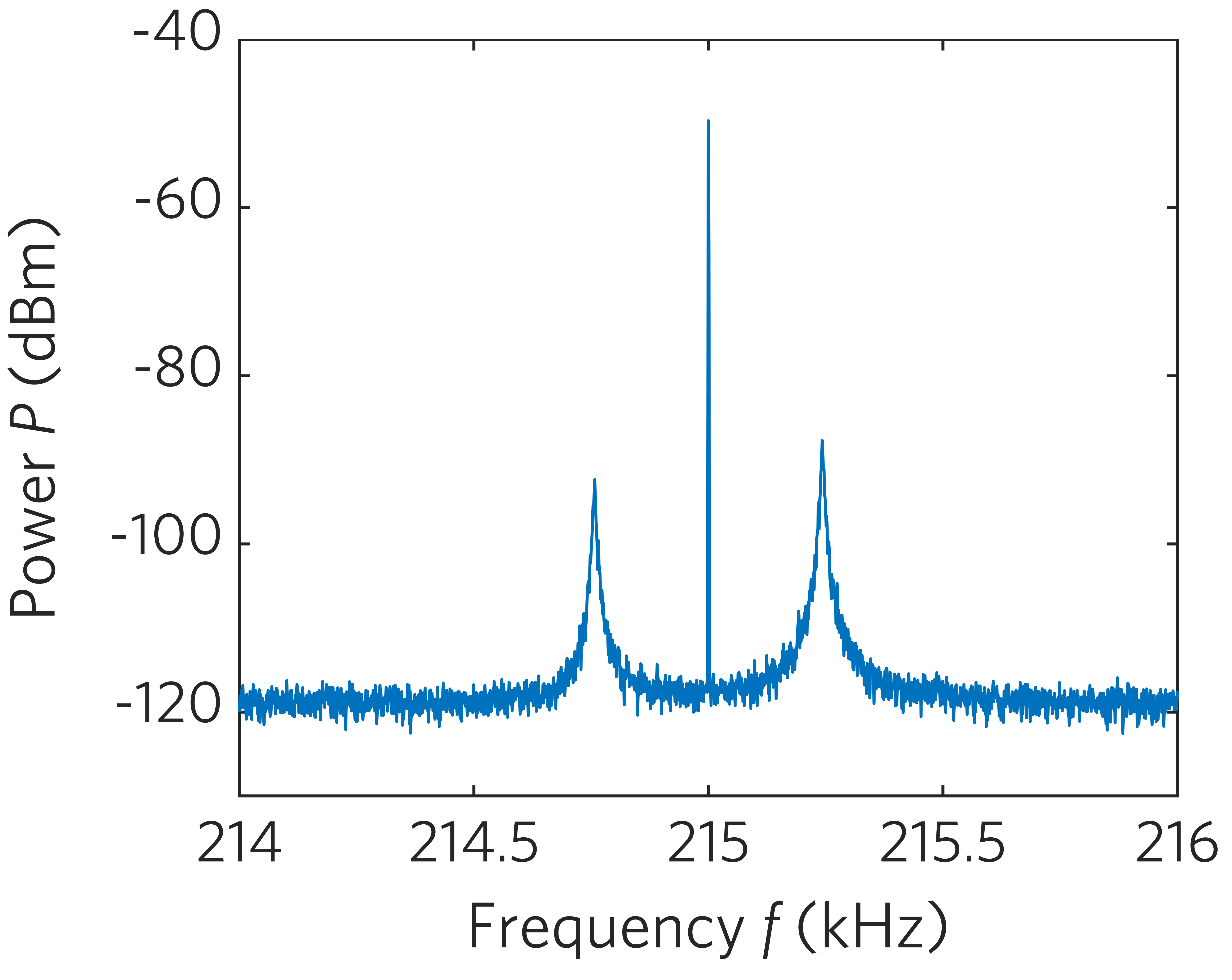


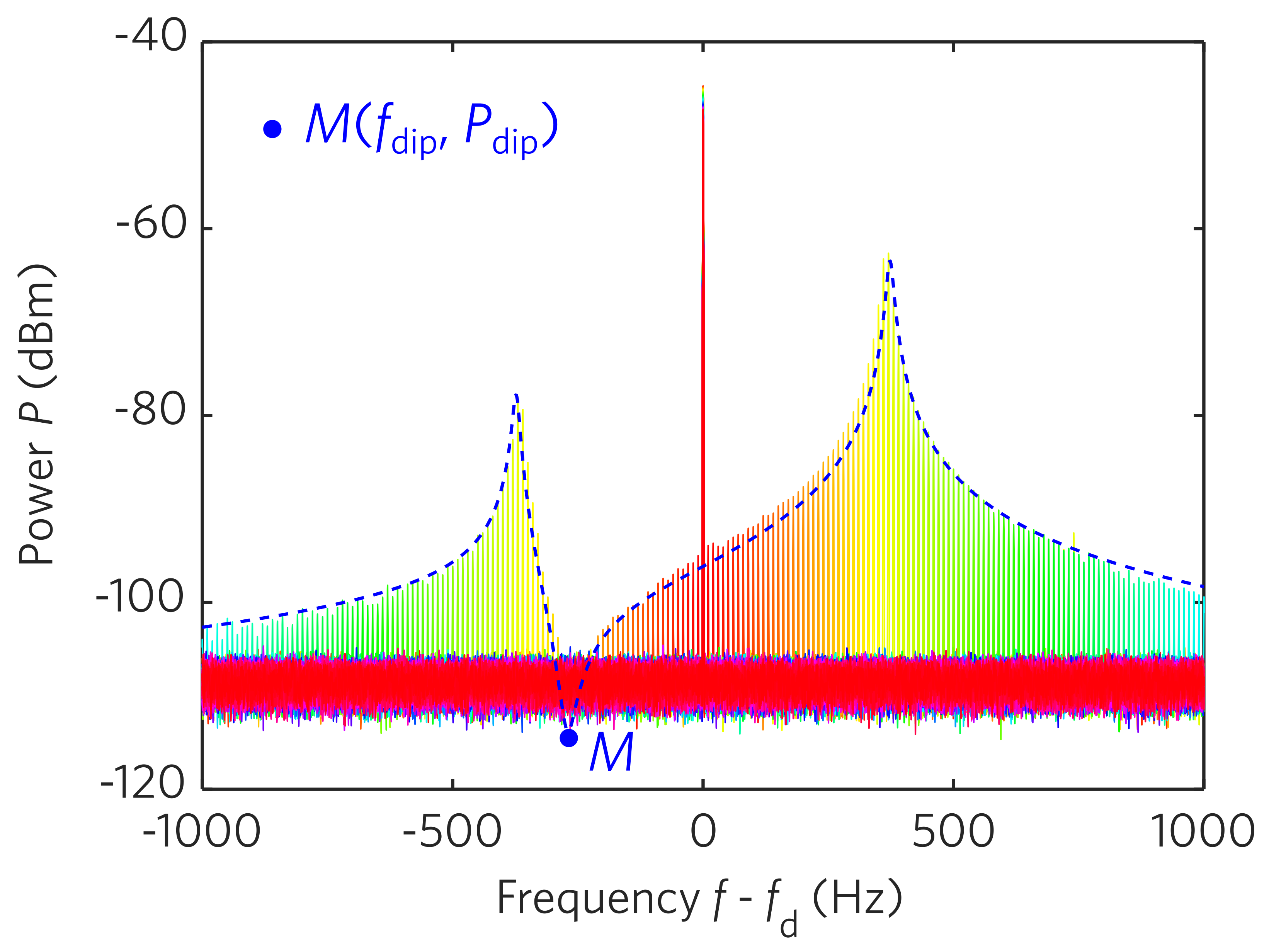
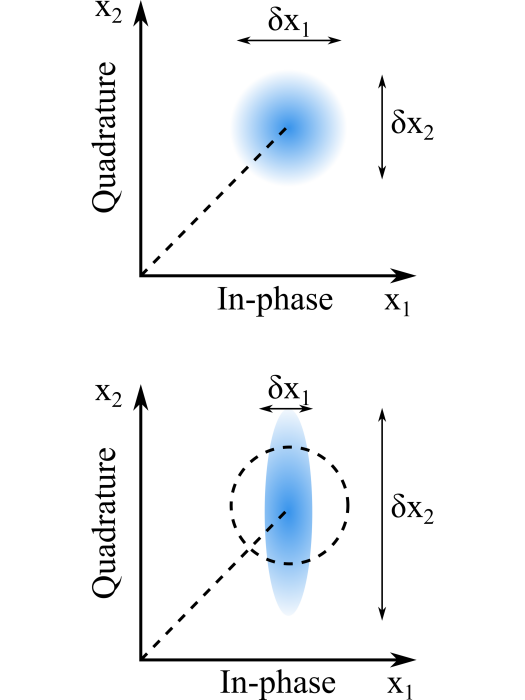
在非線性動力學等非平衡態體系中,環境的隨機擾動在相空間內呈現非均分布,其同相分量漲落被壓縮,正交分量漲落膨脹。該效應被稱為擠壓效應。








在非線性動力學等非平衡態體系中,環境的隨機擾動在相空間內呈現非均分布,其同相分量漲落被壓縮,正交分量漲落膨脹。該效應被稱為擠壓效應。定義 在非線性動力學等非平衡態體系中,環境的隨機擾動(這裡等效於漲落,fluctuati...
①空氣泵氣噪聲 車輛行駛時,輪胎胎面花紋槽與地面耦合形成多個半封閉的空腔。當輪胎與路面接觸時,空腔內的空氣被壓縮而向花紋槽側面開口處流動,形成噴射氣流;當輪胎離開路面時,受擠壓的胎面花紋槽恢復原狀,導致空腔容積迅速恢復而...
輪胎噪聲來自泵氣效應和輪胎振動。所謂自泵氣效應是指輪胎高速轉動時引起的輪胎變形,使得輪胎花紋與路面之間的空氣受擠壓,隨著輪胎滾動,空氣又在輪胎離開接觸面時被釋放,這樣連續的“壓擠釋放”,空氣就迸發出噪聲,而且車速越快噪聲越...
可達100公里每小時)擠壓出去,形成一股低壓氣泡沖流。當這些氣泡破碎時就會發出劇烈的爆裂聲,這種噪聲甚至可以達到200分貝,足以震暈它的獵物!當集群出現時,這種小蝦發出的低壓聲響甚至強烈到可以幫助潛艇規避水下聲納系統的探測。
阮雪榆院士是國際知名的塑性加工和模具技術專家,我國冷擠壓理論與技術的開拓者,在國內外首創冷擠壓許用變形程度理論,並首先研究成功黑色金屬的冷擠壓技術,著有《冷擠壓技術》等4部專著,對指導和推動我國冷擠壓理論與技術的發展做出了...
主要的噪聲源是飛機發動機噪聲和飛機附面層空氣湍流造成的空氣動力噪聲。不同種類的飛機產生的噪聲聲級、頻譜有很大差別。航天員較易感到的噪聲有兩類:發動機系統的噪聲主要是寬頻的,低頻部分聲壓稍高;另一類是太空飛行器通過稠密大氣層邊緣...
擠壓應歸屬於模鍛,可以分為重金屬擠壓和輕金屬擠壓。閉式模鍛和閉式鐓鍛屬於模鍛的兩種先進工藝,由於沒有飛邊,材料的利用率較高。用一道工序或幾道工序就可能完成複雜鍛件的精加工。由於沒有飛邊,鍛件的受力面積就減少,所需要的...
浪面輥壓機,又名擠壓磨、輥壓磨,是國際80年代中期發展起來的新型水泥節能粉磨設備,具有降低鋼材消耗及噪聲的功能,適用於新廠建設,也可用於老廠技術改造,使球磨機系統產量提高30—50%。工作原理 浪面輥壓機是根據料床粉磨原理設計...
腦轉耳鳴,病證名。即頭目眩暈而伴耳鳴。似今之美尼爾氏綜合徵。多由腎虛髓海不足所致。疾病概述 《靈樞·海論》:“髓海不足,則腦轉耳鳴,脛酸眩冒。”疾病症狀 1、環境噪音對傳導性聾患者的聽力干擾輕微,這種患者在噪音較大的...
(1)齒式棘輪機構依靠嚙合傳動,運動可靠;轉角只能作有級調節,機構噪聲較大,承載能力受齒的彎曲與擠壓強度的限制。(2)摩擦棘輪機構依靠摩擦力傳動,運動不準確;轉角可無級調節,噪聲較小,承載能力受工件接觸面強度的限制,結構比齒式...
平模顆粒機型採用皮帶及蝸輪蝸桿兩級傳動,轉動平穩、噪聲低、餵料依靠物料自身的重力,避免堵塞、主軸的轉速約為60rpm,壓輥的線速度約為2.5m/s,可有效去除物料中的氣體,增加了產品的緊密程度。產品介紹 由於線速度較低,同時降低了...
