單李群

在群論中，單李群是一個非標準性的李群。其唯一的理想是0和它自己（或者說，是維度為2或更多維度的李群）。

單李群是一類李群，在類似於簡單群體的離散群體論中發揮著重要的作用。 本質上，單李群是連線的李群，不能被分解為較小連線的李群的擴展，並且不可交換。

與可交換實數的李群R一起，以及單位複數U（1）的簡單李群給出了原子“塊” 通過群擴展的操作來連線所有（有限維）連線的李群。 許多通常遇到的李群是簡單的：例如，對於所有n> 1，具有等於1的n乘n個矩陣的組SL（n）。

一個簡單的李群的等價定義遵循李對應關係：如果李代數簡單，則連線的李群就是簡單的。 一個重要的技術要點是，簡單的李群可能包含離散的正常子群，因此簡單的李群與簡單的抽象群不同。

基本介紹

• 中文名：單李群
• 外文名：Simple Lie group
• 學科：數學
• 性質：非標準性的李群
• 適用場合：離散群體論
• 相關名詞：李群

簡介

在群論中，單李群是一個非標準性的李群。其唯一的理想是0和它自己（或者說，是維度為2或更多維度的李群）。

單李群是一類李群，在類似於簡單群體的離散群體論中發揮著重要的作用。 本質上，單李群是連線的李群，不能被分解為較小連線的李群的擴展，並且不可交換。

與可交換實數的李群R一起，以及單位複數U（1）的簡單李群給出了原子“塊” 通過群擴展的操作來連線所有（有限維）連線的李群。 許多通常遇到的李群是簡單的：例如，對於所有n> 1，具有等於1的n乘n個矩陣的組SL（n）。

一個簡單的李群的等價定義遵循李對應關係：如果李代數簡單，則連線的李群就是簡單的。 一個重要的技術要點是，簡單的李群可能包含離散的正常子群，因此簡單的李群與簡單的抽象群不同。

單李群包括許多古典的李群，它們為費利克斯克萊恩的埃爾蘭根計畫提供了球形幾何，投影幾何和相關幾何的組理論支撐。 在簡單李群的分類過程中出現，也存在幾種與任何熟悉的幾何相對應的特殊可能性。 這些特殊的組織在數學的其他分支以及當代理論物理學中占有許多特殊的例子和配置。

簡單的複數李群

所有李群都是平滑的拓撲空間。 數學家經常研究複雜的李群，它們是底層拓撲空間上具有複雜結構的李群，需要與群操作兼容。 一個複雜的李群如果連線成一個拓撲空間，其李代數是簡單的複數李代數，這就是簡單的問題了。請注意，潛在的李群可能不是簡單的，儘管它仍然是半成品（見下文）。

半代數和還原組

研究比普通組更簡單的李群的一般類，通常是有用的，即簡單的或更普遍的還原性的李群。 如果李代數是半代數，即簡單的李代數的直接和，則連線的李群被稱為半微積分。 如果李代數是簡單（一維）李代數的直接和，則稱為還原。 還原組自然地出現在代數，幾何和物理學中的許多數學對象的對稱性。 例如，n維實數向量空間的對稱性（等價地，可逆矩陣組）的組 是可還原的。

表征理論

來自李群G到矩陣組的拓撲組同態稱為G的表示，簡單李群的表示是稱為表示理論的數學分支的構建塊。 簡單組的有限維表示被劃分為不可約表示的直接和，它們通過滿足某些屬性的權重格子中的向量來分類。

單李群的分類

全分類

單李群完全分類。 分類通常以幾個步驟表示，即：

（1）簡單複數李代數的分類通過Dynkin圖對複數的簡單李代數進行分類。

（2）簡單真實李代數的分類每個簡單的複數李代數有幾種真實形式，在IchirôSatake之後通過其Dynake圖的額外裝飾分類為佐竹圖。

（3）單李群的分類對於每個（真實或複雜）簡單的李代數g，有一個獨特的“無心”單李群G他的李代數是g。

（4）單李群的分類

可以看出，任何一個李群的基本組是一個離散的交換組。給定一些李群G的基本組的（非平凡）子組 ，可以用K來構造一個新的組 在其中心。現在可以通過將這個結構套用到無心的李群中來獲得任何（真實或複雜的）組。請注意，以這種方式獲得的真正的李組可能不是任何複雜組的真實形式。這樣一個真正的群體的一個非常重要的例子就是組合，它出現在無限維表示理論和物理學中。

緊湊的李群

每個單李群具有獨特的真實形式，其對應的無心李群是緊湊的。 事實證明，在這些情況下，簡單連線的李群也很緊湊。 由於Peter-Weyl定理，緊湊李群具有特別易於理解的表示理論。 就像簡單的複數李代數一樣，緊湊的李群被Dynkin圖分類（首先被Wilhelm Killing和ÉlieCartan分類）。

對於無限（A，B，C，D）系列的Dynkin圖，與每個Dynkin圖相關聯的簡單連線的緊湊李群可以被明確地描述為矩陣組，相應的無心緊湊李群被描述為標量矩陣子群。

A系列

A1，A2，...

Ar具有相關聯的緊湊組，特殊單位組SU（r + 1）及其相關緊湊組投影單一組PU（r + 1）。

B系列

B2，B3，...

Br具有相關聯的無心緊湊組合奇數特殊正交組，SO（2r + 1）。 這個組不是簡單的連線：它是通用（雙）旋轉組。

C系列

C3，C4，...

Cr與其相關聯的簡單連線組是一組單一辛矩陣，Sp（r）和其相關聯的無中心組的投影單位辛矩陣的Lie組PSp（r）= Sp（r）/ {I，-I}。

D系列

D4，D5，...

Dr具有相關聯的緊湊組，甚至特殊的正交組，SO（2r）和其相關聯的無心緊湊組投影特殊正交組PSO（2r）= SO（2r）/ {I，-I}。 與B系列一樣，SO（2r）不是簡單的連線; 它的通用封面又是Spin集團，但後者又有一個中心（參見其文章）。

例外情況

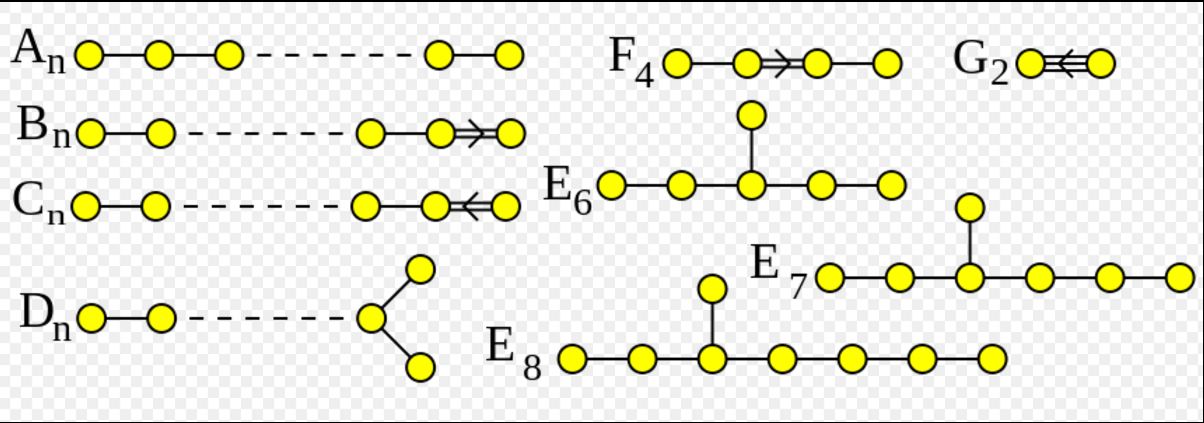
除了上述四個系列，還有五個所謂的特殊Dynkin圖G2，F4，E6，E7和E8。 所有這些也具有相關聯的簡單連線和無心緊湊的組，儘管這些不像在上面的無限系列Ai，Bi，Ci和Di的矩陣組（為什麼）被描述的容易。

簡單組

一個簡單的組合是一個李群，其Dynkin圖只包含簡單的連結，因此相應的李代數的所有非零根具有相同的長度。 A，D和E系列組合都是簡單的，但是沒有B，C，F或G類的組合是簡單的。