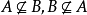充分必要條件

充分必要條件也即充要條件，意思是說，如果能從命題p推出命題q，而且也能從命題q推出命題p ，則稱p是q的充分必要條件，且q也是p的充分必要條件。

如果有事物情況A，則必然有事物情況B；如果有事物情況B，則必然有事物情況A，那么B就是A的充分必要條件 ( 簡稱：充要條件 )，反之亦然 。

基本介紹

• 中文名：充分必要條件
• 外文名：necessary and sufficient conditions
• 類型：概念
• 類別：數學
• 簡稱：充要條件
• 判別方法：充分條件且必要條件

說明

假設A是條件，B是結論

（1）由A可以推出B，由B可以推出A，則A是B的充分必要條件()，或者說B的充分必要條件是A。

（2）由A可以推出B，由B不可以推出A，則A是B的充分不必要條件(A∈B)

（3）由A不可以推出B，由B可以推出A，則A是B的必要不充分條件(B∈A)

（4）由A不可以推出B，由B不可以推出A，則A是B的既不充分也不必要條件()

舉例

1. A=“三角形等邊”；B=“三角形等角”。

2. A=“某人觸犯了法律”；B=“應當依照刑法對他處以刑罰”。

3. A=“付了足夠的錢”；B=“能買到商店裡的東西”。

例1中A是B的充分必要條件；

例2中A是B的必要不充分條件；（A觸犯法律包含各種法，有刑法有民法；B已經確定是刑法。B屬於A所以A是B的必要不充分條件）

例3中A是B的必要不充分條件；（ A付夠了錢 可以買的是車 房子等；但是B能買到超市裡的東西一定是要付夠錢）

生活中

1. 生活中表達充分必要條件的情況不太常見。在邏輯學和數學中一般用“若且唯若”來表示充分必要條件。例如：
   若且唯若競爭對手甲退出投標時，乙才會報一個較高的價位。
   a、b為任意實數時，a²+b² ≥ 2ab 成立，若且唯若a=b時取等號。
   
2. 其他常見的表示充分必要條件的說法還有：“需要且只需要”、“唯一條件”的情況。例如：
   任何兩個端節點之間的轉發需要且只需要經過三次交換。
   為了防止圓管內流動的水發生結冰，則需要且只需要保持圓管內壁面的最低溫度在某一溫度以上。
   俄軍逼近格首都稱停火唯一條件是格軍放棄武力。
   

邏輯學中

定義：如果有事物情況A，則必然有事物情況B；如果沒有事物情況A，則必然沒有事物情況B，A就是B的充分必要條件。

充分必要條件是邏輯學在研究假言命題及假言推理時引出的。

陳述某一事物情況是另一件事物情況的充分必要條件的假言命題叫做充分必要條件假言命題。充分必要條件假言命題的一般形式是：p若且唯若q。符號為：p←→q(讀作“p等值q”) 。

例如：“三角形等邊若且唯若三角形等角。”是一個充分必要條件假言命題。

根據充分必要條件假言命題的邏輯性質進行的推理叫充分必要條件假言推理。

數學中

有命題p、q，如果p推出q且q推出p，則p是q的充分必要條件，簡稱充要條件。

p推出q，p是q的充分條件，同時q是p的必要條件，此時p是q的子集。

例如：a、b一正一負推出ab<0，ab<0推出a、b一正一負，則a、b一正一負和ab<0互為充要條件。

簡單的說就是在證p與q時,前面那個推出後面那個就是充分條件；後面那個推出前面那個就是必要條件；前面能推出後面、後面也能推出前面就是充要條件。

對於“若p則q”形式的命題，如果已知pq，那么p是q的充分條件，q是p的必要條件。

例如，如果a+i²=-1，則a=0，因此，a+i²=-1是a=0的充分條件，a=0是a+i²=-1的必要條件。（註：i²=-1，i為虛數。）

如果既有p推出q，又有q推出p，則記作p=q，就說p是q的充要條件，也可以說q是p的充要條件，或者若p推出q，但q推不出p，則p是q的充分不必要條件，q是p的必要不充分條件。

例如“兩個三角形全等”是“兩個三角形面積相等”的充分不必要條件，|x|=|y|是“x²=y²”的充要條件。