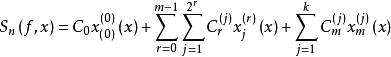哈爾正交系

哈爾正交系是哈爾於1910年所建立的一個正交函式系。哈爾函式的全體成為[0,1]上的一個完備的規範正交系，稱為哈爾正交系。

基本介紹

• 中文名：哈爾正交系
• 外文名：Haar orthogonal system
• 適用範圍：數理科學

簡介

哈爾正交系是哈爾於1910年所建立的一個正交函式系。

哈爾函式

定義

對於正整數 m 及 ，令

在(0,1)的其他點上，定義， 為其左、右極限的算術平均值，又定義 為 在 中的值， 為 在 中的值，稱 為哈爾函式。

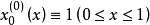
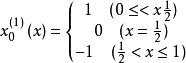
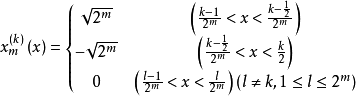
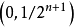
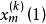
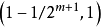
定義

哈爾函式的全體成為[0,1]上的一個完備的規範正交系，稱為哈爾正交系。

推廣

對於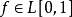 ，稱

為 f(x) 的哈爾展開式，也稱為 f(x) 關於哈爾系的傅立葉級數，這裡

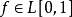
f(x)的哈爾展開式不僅在[0,1]上幾乎處處收斂於f(x)，而且在f(x)的連續點上一定收斂於f(x)，此外，在f(x)的一致連續的區間上，此展開式還一致收斂於f(x)。

任給正整數 n，記，稱

為f(x)的哈爾展開式的第 n 部分和 是一種逼近工具，若，記為f(x)的連續性模，則存在常數 C>0，使得