基本介紹
- 中文名:反演點
- 外文名:inversion point
- 所屬學科:數學(幾何學)
- 相關概念:反演,反演變換等
- 反演點:和在數學和物理中有很重要的套用
基本解釋,相關解釋,
基本解釋
解釋1 設有一個圓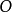 ,其半徑等於R,對於所在平面上異於
,其半徑等於R,對於所在平面上異於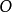 的任一點
的任一點 ,在射線
,在射線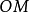 上存在一點
上存在一點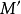 ,滿足
,滿足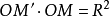 ,我們把點
,我們把點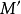 叫做點
叫做點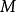 關於圓
關於圓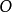 的反演點。顯然點
的反演點。顯然點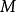 也是點
也是點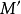 關於圓
關於圓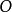 的反演點,因此說點
的反演點,因此說點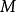 和點
和點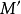 關於圓互為反演點。對於一個平面圖形,我們把一個圖形上的任一點變換成它的關於一已知圓的反演點的變換叫做反演變換,簡稱反演。這裡,已知的圓叫做反演圓,已知圓的中心叫做反演極,已知圓的半徑叫做反演半徑,半徑的平方叫做反演冪。
關於圓互為反演點。對於一個平面圖形,我們把一個圖形上的任一點變換成它的關於一已知圓的反演點的變換叫做反演變換,簡稱反演。這裡,已知的圓叫做反演圓,已知圓的中心叫做反演極,已知圓的半徑叫做反演半徑,半徑的平方叫做反演冪。
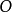
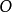

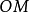
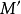
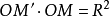
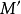
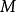
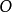
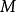
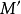
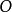
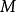
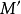
還可以仿上法去定義空間的圖形關於一個已知球的反演(這時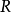 為球半徑)、平面或是空間的圖形關於一個已知點
為球半徑)、平面或是空間的圖形關於一個已知點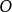 的反演(這時只須改成
的反演(這時只須改成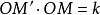 是常數)。
是常數)。
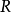
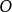
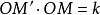
對於一個變換,由這一變換下的象出發,反過來求其原象的過程,叫做這一變換的反演。
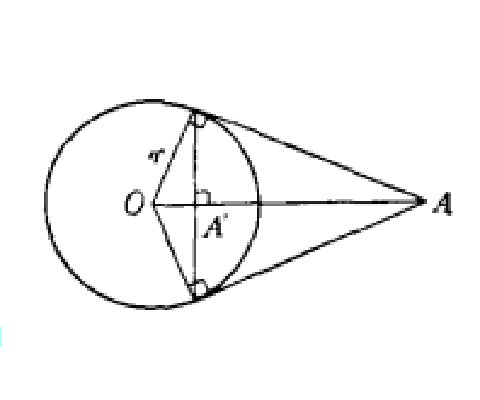
解釋2 在平面上取定點 ,以
,以 為中心、
為中心、 為半徑作圓,又取
為半徑作圓,又取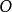 以外的任意點
以外的任意點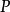 ,用直線連線
,用直線連線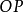 ,在半直線
,在半直線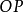 上取點
上取點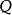 ,使
,使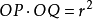 。
。



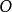
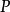
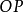
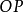
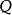
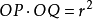
 圖1
圖1這時,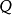 稱為
稱為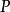 的反演點,使
的反演點,使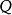 對應於
對應於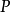 的對應稱為反演。這時所作的圓稱為反演圓,該圓的半徑稱為反演半徑,圈心
的對應稱為反演。這時所作的圓稱為反演圓,該圓的半徑稱為反演半徑,圈心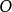 稱為反演中心。通過反演,反演圓內部的點變到外部的點,外部的點變到內部的點,而反演圓的圓周上的點不變。在空間中,對於球面,可與平面的情況一樣地定義反演。
稱為反演中心。通過反演,反演圓內部的點變到外部的點,外部的點變到內部的點,而反演圓的圓周上的點不變。在空間中,對於球面,可與平面的情況一樣地定義反演。
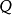
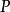
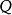
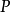
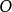
相關解釋
若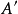 為以定點
為以定點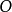 為端點的射線
為端點的射線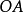 上一點,且
上一點,且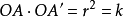 (
(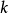 為非零常數),則稱
為非零常數),則稱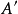 為
為 關於
關於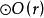 的反演點,同樣,
的反演點,同樣,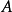 為
為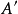 關於
關於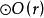 的反演點。定點
的反演點。定點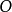 稱為反演中心,
稱為反演中心, 為反演半徑,
為反演半徑,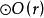 為反演基圓,
為反演基圓,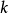 為反演冪。若
為反演冪。若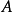 經變換而變為它的反演點
經變換而變為它的反演點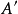 ,則稱此變換為反演變換。
,則稱此變換為反演變換。
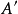
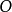
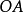
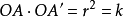
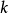
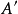

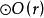
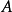
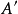
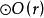
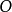

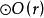
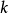
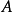
若圖形F上各點經反演變換得圖形F’,則稱F和F’互為反像。反演中心不存在反演點,若F和F'不包含反演中心,則F與F’的點一一對應。經過反演中心的直線為二重線;反演基圓上的點為二重點。當反演基圓變態為直線時,此時反演中心不復存在,反演變換相應變態為反射.反演變換有以下重要定理:
(1)不共線的兩雙反演點共圓,且此圓與反演基圓正交;
(2)不通過反演中心的直線,其反像為過反演中心的圓,其逆亦真;
(3)不通過反演中心的圓,其反像亦為不通過反演中心的圓;
(4)與反演基圓正交的圓,其反像為原圓;
(5)兩條曲線在某交點的交角,經反演,大小不變,方向相反,正交兩圓其反像仍正交;相切兩圓的反像仍相切,若切點恰是反演中心,則其反像為兩平行線;一直線若與一圓相切,其反像亦仍相切。
反演變換因其具有上述性質而成為證題和作圖中的重要工具,通常研究的反演變換,反演冪k為大於零的數,若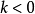 ,則反演基圓為虛圓,上述性質則不復存在,對於此類反演變換可轉化為反演冪為
,則反演基圓為虛圓,上述性質則不復存在,對於此類反演變換可轉化為反演冪為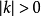 的反演變換和一次點反射的積來代替。
的反演變換和一次點反射的積來代替。
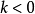
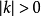
 圖2
圖2