反常擴散(anomalous diffussion)是一種複雜系統的擴散過程。即不再遵循高斯統計,Fick第二定律不能夠描述其相應的輸運行為。
基本介紹
- 中文名:反常擴散
- 外文名:Anomalous diffusion
- 釋義:與時間不成線性關係的擴散過程
- 類屬:物理學
介紹,定義,分類,描述方法,
介紹
定義
作為一個隨機過程,布朗微粒的正常擴散是中心極限定理的直接結果,該輸運過程遵循統計表現為其均方位移與時間的線性依賴關係: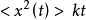
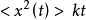
其中k為擴散係數,然而許多複雜系統的擴散過程通常不再遵循高斯統計,即Fick第二定律不能夠描述相應的輸運行為這種現象被稱為反常擴散(anomalous diffussion)。
大量的實驗表明,反常擴散現象在自然界中普遍存在,該現象在物理、化學、生物等領域的各種複雜系統中被頻繁觀測到,不同於經典擴散,反常擴散不再遵守Fick定律或Fourier定律,反常擴散微粒的均方位移表現為與時間的非線性依賴關係:

分類
其中 為反常擴散指數,
為反常擴散指數,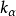 為反常擴散係數,根據反常擴散指數,反常擴散分為次擴散、正常擴散、超擴散、彈道擴散。特別地,來源於粒子與熱浴之間的相互作用,其均方位移是發散的,也是反常擴散的一種情形。
為反常擴散係數,根據反常擴散指數,反常擴散分為次擴散、正常擴散、超擴散、彈道擴散。特別地,來源於粒子與熱浴之間的相互作用,其均方位移是發散的,也是反常擴散的一種情形。

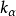
描述方法
近年來,反常擴散現象引起人們的廣泛關注經典的擴散表現為布朗微粒的局域性運動,而反常擴散則表現為布朗微粒的非局域性(時間和空間)運動大量有效的方法和模型被用來描述這一現象。
主要包括:分數布朗運動、廣義的擴散方程、連續時間隨機行走模型、Langevin方程、廣義的Langevin方程、廣義主方程方法、Tsalli統計等,上述描述反常擴散的方法和模型中,只有連續時間隨機行走模型和廣義的Langevin方程結合了系統的記憶性質且其機率密度函式均有一致的表達式雖然連續時間隨機行走模型清晰地描述了粒子的運動軌跡,但是該模型只與系統的統計性質有關,不涉及系統的動力學行為且該模型無法直接引入力場和邊界(或無法直接在相空間中考慮所研究微粒的動力學行為作為描述反常擴散動力學的另一個合理選擇,分數階動力學方程則可以直接引入外力場並能靈活地處理邊界

