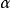參數多態(parametric),採用參數化模板,通過給出不同的類型參數,使得一個結構有多種類型。
基本介紹
簡介,歷史,直謂與非直謂,直謂多態,非直謂多態,限定的參數多態,特設多態,
簡介
參數多態在程式設計語言與類型論中是指聲明與定義函式、複合類型、變數時不指定其具體的類型,而把這部分類型作為參數使用,使得該定義對各種具體類型都適用。參數化多態使得語言更具表達力,同時保持了完全的靜態類型安全。這被稱為泛型函式、泛型數據類型、泛型變數,形成了泛型編程的基礎。
參數多態名字來源於其發明人克里斯托弗·斯特雷奇,與特設多態(ad hoc polymorphism)相對。特設多態是指一個多態函式有多個不同的實現,依賴於其實參而調用相應版本的函式。因此,特設多態僅支持有限數量的不同類型。
歷史
克里斯托弗·斯特雷奇於1967年8月在哥本哈根的電腦程式設計暑期學校發表了著名論文Fundamental Concepts in Programming Languages中首次提出了參數多態、特設多態、左值、右值等概念。1975年ML語言首次實現了參數多態。
現在,Standard ML,OCaml,F#,Ada,Haskell,Mercury,Visual Prolog,Scala,Julia等。Java,C#,Visual Basic .NETandDelphi引入了泛型作為參數多態。
直謂與非直謂
直謂多態
非直謂多態
非直謂多態(Impredicative polymorphism),也稱“頭等多態”(first-class polymorphism)是最強有力的參數多態形式。非直謂是指自引用(self-referential),類型論中允許實例化類型 的變數為任何類型,包括參數化類型,如
的變數為任何類型,包括參數化類型,如 自身。一個例子是系統F在類型變數X下,類型
自身。一個例子是系統F在類型變數X下,類型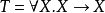 ,其中X可以為T自身。
,其中X可以為T自身。


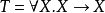
限定的參數多態
1985年盧克·卡德利與彼得·華格納提出類型參數允許限定(bounds)的益處。限定量化(bounded quantification)也稱作“限定多態”(bounded polymorphism)或“約束泛型”(constrained genericity)。許多操作要求數據類型的某些知識,但仍可以把類型參數化。例如,判斷一項是否出現在列表中,需要比較項的相等。在Standard ML中,類型參數’’a被限定有相等判斷可用,因此具有如下類型的函式:’’a×’’alist → bool且’’a可譯為任何定義了任何定義了相等判斷的類形。在Haskell中,限定是通過要求類型屬於某個type class,因此同樣的函式在Haskell中可寫為: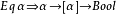 。大多數支持參數多態的面向對象語言可以把參數限定為給定類型的子類型。
。大多數支持參數多態的面向對象語言可以把參數限定為給定類型的子類型。
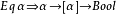
特設多態
特定多態(ad hocpolymorphism)是程式設計語言的一種多態,多態函式有多個不同的實現,依賴於其實參而調用相應版本的函式。因此,特設多態僅支持有限數量的不同類型。函式重載乃至運算符重載也是特設多態的一種。
特定多態的名字來源於其發明人克里斯托弗·斯特雷奇於1967年8月在哥本哈根的電腦程式設計暑期學校發表了著名論文Fundamental Concepts in Programming Languages中首次提出了參數多態、特設多態、左值、右值等概念。。特設多態與參數多態相對。ad hoc在這裡並不是貶義,而是指這類多態並不是類型系統的基本特性,不是像參數多態那樣適用於無窮多的類型,而是針對特定問題的解決方案。
換言之,參數多態對各模板參數的實現,是根據模板的通用(generically)的行為的抽象,即泛型的語義;而特設多態可以針對不同的版本實現完全不同的行為,或曰對於每個不同的模版參數都有單獨的版本來應對。打個比方:假如我們要把原材料切成兩半——
- 參數多態:只要能“切”,就用工具來切割它;
- 特設多態:根據原材料是鐵還是木頭還是什麼來選擇不同的工具來切。