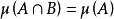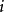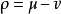基本介紹
- 中文名:原子測度
- 外文名:atomic measure
- 所屬學科:數學(測度論)
- 相關概念:原子,測度空間,非原子測度等
定義,相關介紹,
定義
如果 是一個測度空間,集合
是一個測度空間,集合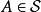 稱為
稱為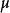 的一個原子(atom),若且唯若
的一個原子(atom),若且唯若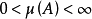 且對每個
且對每個 ,或者
,或者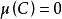 或者
或者 。沒有任何原子的測度稱為非原子的(nonatomic)。
。沒有任何原子的測度稱為非原子的(nonatomic)。

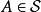
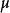
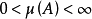

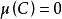

原子的主要實例是具有正有限測度的單元素集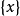 ,一個正的有限測度集合是一個原子,如果它的可測子集僅僅是它本身和
,一個正的有限測度集合是一個原子,如果它的可測子集僅僅是它本身和 ,這裡指非平凡原子:設X是不可數集,
,這裡指非平凡原子:設X是不可數集, 是集合A的集類,A或者可數,滿足
是集合A的集類,A或者可數,滿足 ,或者具有可數補集,滿足
,或者具有可數補集,滿足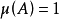 ,那么
,那么 是一個測度,X是一個原子,另一方面,勒貝格測度是非原子的。
是一個測度,X是一個原子,另一方面,勒貝格測度是非原子的。
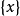



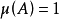

一個測度空間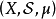 ,或測度
,或測度 稱為純原子的(purely atomic),若且唯若存在由
稱為純原子的(purely atomic),若且唯若存在由 的原子組成的集類
的原子組成的集類 ,使得對每個
,使得對每個 ,
,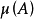 是對所有的
是對所有的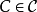 ,滿足
,滿足 的數
的數 的和。(對任意的非負實數
的和。(對任意的非負實數 ,
,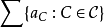 定義為
定義為 上所有有限子集的和的上確界)。純原子測度的主要例子是,存在一個函式
上所有有限子集的和的上確界)。純原子測度的主要例子是,存在一個函式 ,使得
,使得 ,滿足
,滿足 的計數測度是純原子的,在
的計數測度是純原子的,在 上,研究最多的純原子測度集中在對於某個
上,研究最多的純原子測度集中在對於某個 ,滿足
,滿足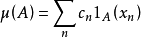 的可數集
的可數集 。
。




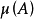
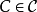



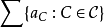






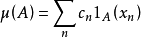

相關介紹
人們對具有無限測度的集合併不感興趣的,它可能會帶來一些技術困難,除非它們有任意大有限測度的子集,對 -有限測度和下面較為一般的個別測度,這也成立。測度空間
-有限測度和下面較為一般的個別測度,這也成立。測度空間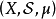 稱為可局部化的(localizable),若且唯若存在由具有有限測度的不相交可測集組成的集類
稱為可局部化的(localizable),若且唯若存在由具有有限測度的不相交可測集組成的集類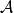 ,這些子集的並為
,這些子集的並為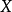 ,使得對每個
,使得對每個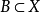 ,
, 是可測的若且唯若對所有
是可測的若且唯若對所有 ,有
,有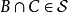 ,從而有
,從而有 ,最有用的可局部化測度是滿足
,最有用的可局部化測度是滿足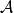 可數的
可數的 -有限測度。在可能不可數集合上的計數測度提供了其他的例子。
-有限測度。在可能不可數集合上的計數測度提供了其他的例子。

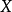
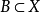


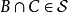

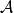

在實際中考慮較多的測度或者是純原子的或者是非原子的,但總可以把一個純原子的有限測度添加到一個非原子測度中,從而得到一個測度,對這個測度,下面的分解是非平凡的。
定理 設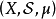 是一個可局部化空間,那么存在
是一個可局部化空間,那么存在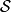 上的測度
上的測度 和
和 ,使得
,使得 ,其中
,其中 是純原子的,
是純原子的, 是非純原子的。
是非純原子的。
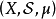
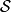





證明提示:首先,可以歸約為有限測度空間的情形,設 為
為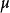 的所有原子組成的集類,對原子
的所有原子組成的集類,對原子 ,定義關係
,定義關係 ,若且唯若
,若且唯若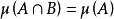 ,這是個等價關係,設
,這是個等價關係,設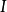 是所有等價類的集合且對每個
是所有等價類的集合且對每個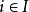 ,在等價類
,在等價類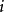 中選擇一個原子
中選擇一個原子 ,令
,令 ,且
,且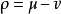 。
。