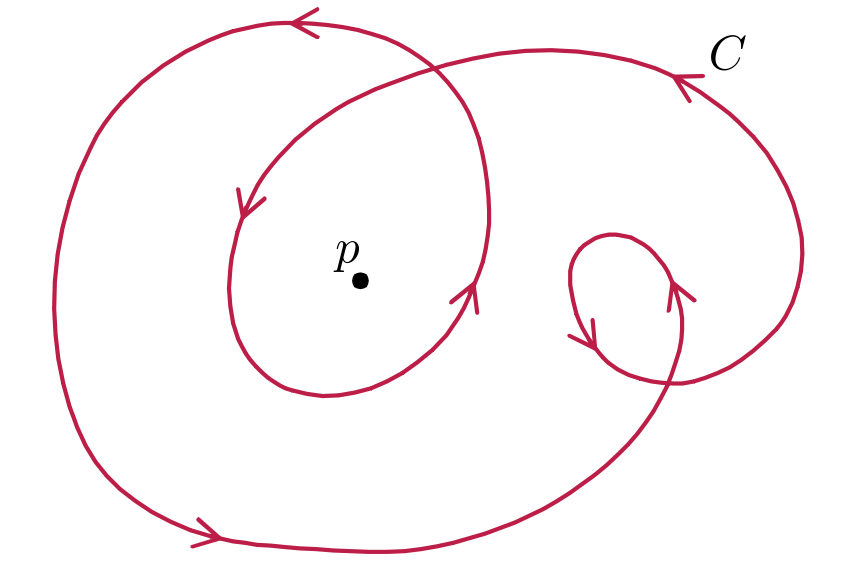
直觀描述
假設在xy平面上有一條有向的閉曲線。我們可以把曲線想像為某個物體的運動軌跡,運動方向就是曲線的方向。曲線的卷繞數就是物體逆時針繞過原點的總次數。
計算繞過原點的總次數時,逆時針方向的運動算正數,順時針方向的運動算負數。例如,如果物體首先依逆時針方向繞過原點四次,然後再依順時針方向繞過原點一次,那么曲線的卷繞數就是3。
利用這種方案,根本不繞過原點的曲線的卷繞數就是零,而順時針繞過原點的曲線的卷繞數就是負數。因此,曲線的卷繞數可以是任何整數。以下的圖中顯示了卷繞數為-2、-1、0、1、2和3的曲線:

卷繞數分別為-2、-1、0、1、2和3的曲線。
形式定義
x-y平面上的曲線可以用參數方程來定義:
如果我們把參數
t視為時間,那么這個方程就描述了物體在
t=0 和
t=1 期間在平面上的運動。只要函式
x(
t) 和
y(
t) 是連續的,運動的軌跡就是一條曲線。只要物體的位置於
t=0 和
t=1 時相同,這條曲線就是閉曲線。
我們可以用極坐標系來定義這種曲線的卷繞數。假設曲線不經過原點,我們可以把參數方程寫成極坐標的形式:
函式
r(
t) 和
θ(
t) 必須是連續的,
r>0。因為最初和最終的位置是相同的,所以
θ(0) 和
θ(1) 的差必須是 2
π 的整數倍。這個整數就是卷繞數:
這個公式定義了 x-y 平面上曲線關於原點的卷繞數。把坐標系平移,我們就可以把這個定義推廣到關於任意一點 p 的卷繞數。
迴轉數
我們也可以考慮路徑關於其自身正切的卷繞數。路徑隨著時間的推移而變化,迴轉數可定義為速度矢量關於原點的卷繞數。於是,在本文開頭所給的示例中,其迴轉數為3,因為計算的是小環路。
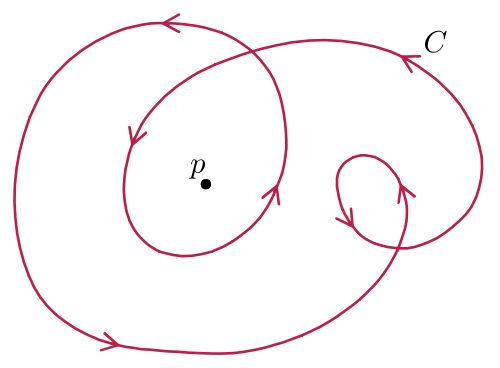
該曲線關於p的卷繞數為2,但它的總曲率為6π,故迴轉數為3。
這僅適用於浸入路徑(immersed path,即導數處處非零的可微路徑),是切向高斯映射的映射度。
這種計算曲線正切旋轉次數的卷繞數稱之為迴轉數(turning number)、旋轉數(rotation number)、旋轉指數(rotation index)或曲線指標(index of the curve),可以用總曲率除以 2π 來計算。