半內積

半內積(semi-inner product)抽象空間微分方程理論的基本概念。

在數學中，半內積是由Gunter Lumer提出的內積的泛化，目的是為了將希爾伯特空間類型參數擴展到泛函分析中的巴納赫空間。吉爾斯後來探索了半內積的基本性質。

基本介紹

• 中文名：半內積
• 外文名：semi-inner product
• 領域：數學
• 提出者：Gunter Lumer
• 屬性：內積的泛化
• 相關名詞：內積

簡介

在數學中，半內積是由Gunter Lumer提出的內積的泛化，目的是為了將希爾伯特空間類型參數擴展到泛函分析中的巴納赫空間。吉爾斯後來探索了半內積的基本性質。

定義

這裡給出的定義與標準函式分析教科書中的“半內積”不同，“半內積”滿足內積的所有性質(包括共軛對稱)，但不要求嚴格為正。

複數域C上的線性向量空間的V的半內積是一個從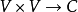 中的函式。通常表示成 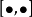，因此：

並且 若且唯若

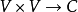
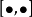
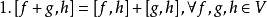
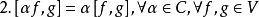
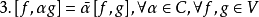
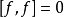
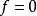
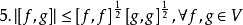
與內積空間的區別

半內積與內積的不同之處在於它一般不是共軛對稱的，即，

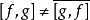
通常。 這相當於說

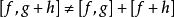
換句話說，半內積對於其第二變數通常是非線性的。

巴拿赫空間的半內積

如果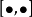 是線性向量空間V的半內積，那么

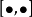
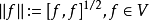
在V上定義了一個範數。

相反，如果V是具有範數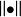 的規範向量空間，那么在V上總是存在（不可能是唯一的）與V上的規範一致的半內積，這意味著

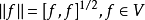
套用

（1）根據Lumer的想法，半內積廣泛套用於研究巴拿赫空間的有界線性運算元；

（2）2007年，Der和Lee套用半內積在巴拿赫空間開發大幅度分類；

（3）近來，半內積已被用作建立機器學習中再現核心巴拿赫空間的概念的主要工具；

（4）半內積也可用於建立框架理論，Riesz基礎為巴拿赫空間。