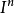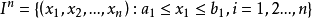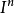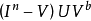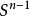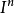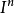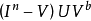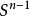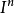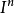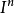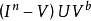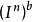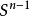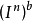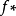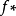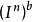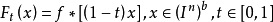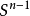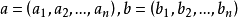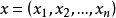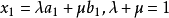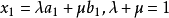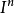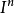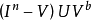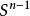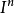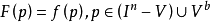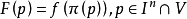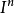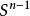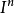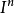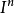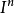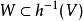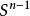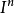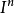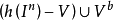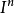設X是拓撲空間，M包含於X，h是從x到X的同胚。易證，如果x是M的內點，則h(x)仍為h(M)的內點，如果x是M的邊界點，則h(x)仍為h(M)的邊界點。但是，如果h只在M上定義，則邊界點或內點未必是不變的。例如，設X是E3空間中由平面(x1，x2，0)及x3軸組成，M是X中由x3軸組成的子集。h是一從x3軸到x1軸的同胚映射，則點(0，0，1)是M的一個內點，但它的象h(0，0，1)不再是h(M)的內點，因為，在X中不存在包含點h(0，0，1)而完全含於h(M)的開集。然而，對於歐氏空間來說，不會發生這種情形，內點的同胚象必仍為內點，邊界點的同胚象必仍為邊界點。這個定理，就是區域不變性定理。
基本介紹
- 中文名：區域不變性定理
- 外文名：Regional invariance theorem
- 領域：數學
- 作用範圍：拓撲空間
- 性質：邊界點的同胚象必仍為邊界點
- 相關名詞：同胚映射
簡介,區域不變性定理的簡化證明,引理A,引理B,
簡介
設X是拓撲空間，M包含於X，h是從x到X的同胚。易證，如果x是M的內點，則h(x)仍為h(M)的內點，如果x是M的邊界點，則h(x)仍為h(M)的邊界點。但是，如果h只在M上定義，則邊界點或內點未必是不變的。例如，設X是E3空間中由平面(x1，x2，0)及x3軸組成，M是X中由x3軸組成的子集。h是一從x3軸到x1軸的同胚映射，則點(0，0，1)是M的一個內點，但它的象h(0，0，1)不再是h(M)的內點，因為，在X中不存在包含點h(0，0，1)而完全含於h(M)的開集。然而，對於歐氏空間來說，不會發生這種情形，內點的同胚象必仍為內點，邊界點的同胚象必仍為邊界點。這個定理，就是區域不變性定理。
區域不變性定理的簡化證明
定義歐氏空間En的方體
為
則下列兩引理成立
引理A
對於 的內點x，不論點x的鄰域V(x)如何小，存在從
到
的連續映射：
不能連續地擴張到 。
引理B
對於 的邊界點x，存在點x的小鄰域V(x)，不論從 到 的連續映射如何，均能連續地擴張到 。
為了證明引理A，用反證法。假設相反，x是 的內點，取閉包含於二 的球鄰域為V(x)，取f為以x為投影中心從
到
(與
同胚)的中心投射。顯然，f使
的點不動。如果存在f的連續擴張
，則 仍使 的點不動。
考慮連續映射F，:
則常值映射F1(x)與恆等映射Fo(x)同倫，然而這是不可能的。下面我們來證明常值映射F1(x)與恆等映射Fo(x)不能同倫。為了方便起見，假設Ft是定義在
球面之上的。
設
是歐氏空間En的兩個點，則En的所有滿足下列條件的點
：
的集合記為(a,b)，稱為以a，b為端點的線段。歐氏空間En的子集合M稱為凸的，若且唯若a∈M，b∈M蘊涵(a,b)cM。
為了證明引理B，設x是 的任一個邊界點，取以x為中心不完全包含 的球鄰域V。設f是從
到
的任一個連續映射。由於x是邊界點，必存在一屬於V而不屬於
的點q，以q為中心將
向Vb投射，以二記此中心投影，顯然二是連續映射。考慮連續映射F：
於是F(P)是一從 到 的連續映射，而且F是f的連續擴張。
由於x是M的內點，故必存在一以x為內點完全含於M中的小方體。如果h(x)不是11(M)的內點，則h(x)更不是h()的內點，因而是h()的邊界點。由引理B，存在h(x)的開鄰域V，滿足引理B的條件。又因h為同胚映射，故對於h(x)的開鄰域V，存在x的開鄰域Wc，使
。由引理A，存在從
到的連續映射f，不能連續擴張到。然而，另一方面，將引理B運用於h()的邊界點h(x)及開鄰域V，考慮連續映射fh-1，對於
的任一點y，
。可知fh-1能連續地擴張到h(r)，因此，f也能連續地擴張到。得出矛盾。所以，h(x)不能是h(M)的邊界點。證完。
