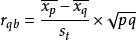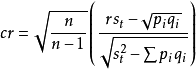區分度，是指一個測驗題目能夠在多大程度上區分所要測量的心理品質，反映了測驗題目對心理品質區分的有效性。一個具有良好區分度的題目，在區分被測者時應當是有效的。能通過該項目或是在該項目上得分高的被測者，其對應的品質也較突出；反之，區分度較差的項目就不能有效地鑑別水平高或低的被測者。因此，區分度也叫做項目的效度，並作為評價項目質量、篩選項目的主要依據。
區分度的計算以被測者對項目的反應與某種參照標準之間的關係為基礎，其取值範圍是-1.00~+1.00。一般情況下，區分度應為正值，稱作積極區分，值越大則區分度越好；若區分度為負值，則為消極區分，說明這個題目有問題，應刪除或重新修訂；區分度為0，為無區分作用。
基本介紹
- 中文名：區分度
- 外文名：discrimination
- 別稱：項目的效度
- 用途：評價項目質量、篩選項目
- 取值範圍：-1.00~+1.00
- 特徵：相對性
概念,相對性,區分度的指標及計算,區分度指數,相關係數法,項目特徵曲線,區分度和難度,
概念
區分度（discrimination）是指測驗項目對於所研究的受測者的心理特性的區分程度或鑑別能力。區分度高的項目，能將不同水平的受測者區分開來，能力強、水平高的受測者得分高，能力弱、水平低的受測者得分低；區分度低的項目，就沒有很好的鑑別能力，水平高和水平低的受測者得分差不多。
區分度是指測驗題目對所要測量的心理特性的靈敏度或鑑別能力。凡是區分度較好的題目，則能將不同水平的被試區別開來。題目的區分度從實質上講就是題目本身的效度。題目的區分度是評價題目質量好壞的一個重要指標，也是篩選題目的主要依據。
項目區分度（item discrimination）是指項目對不同水平的被試的區分程度。項目區分度分析可以分為兩種類型：一種是“項目效度”的分析，根據外部校標選取題目，適用於人格測驗；另一種是“內部一致性”分析，根據測驗總分選取題目，適用於教育成就測驗和能力傾向測驗。
相對性
1）採用不同的計算方法，區分度的值也有所不同。因此，在分析一份測驗題目的區分度時，對同一類型的題目須採用同一種計算題目區分度的方法，結果才好相互比較，進而篩選題目。
2）一個題目區分度的大小受被試團體異質程度的影響。被試團體越同質，同一題目的區分度值越小；若被試團體越異質，同一題目區分度則越大。因此，在說明題目區分度時總是針對某個具體的被試團體而言，離開具體的被試團體一般地、抽象地談題目的區分度是沒有任何意義的。
3）用相關法計算題目區分度的可靠性受樣本大小的影響。一般而言，樣本越大，區分度值越可靠。但樣本太大，反而增加計算量，也毫無實際意義，應適可而止。
由於區分度具有相對性，很難確定一個絕對水平作為取捨題目的標準。在根據題目區分度來篩選題目時，總要考慮到測驗的目的和功能。於學科測驗而言，一般要求相關係數達到顯著性水準，或區分度指數D值在0.20以上，國際上優秀題目的區分度要求達到0.40以上。若是一個選拔人才的測驗，題目的區分度要儘量高一些。美國教育與心理測量學家艾伯（L. Ebel）根據區分度指數提出一個評價題目優劣的標準，見表1-1。
區分度指數（D） | 試題評價 |
0.40分以上 | 非常優良 |
0.30-0.39 | 良好 |
0.20-0.29 | 尚可，須修改 |
0.19以下 | 劣，必須淘汰 |
區分度的指標及計算
區分度的常用指標為D，取值在-1～1之間，值越大區分度越好。測量學家伊貝爾認為：試題的區分度在0.4以上表明此題的區分度很好，0.3～0.39表明此題的區分度較好，0.2～0.29表明此題的區分度不太好需修改，0.19以下表明此題的區分度不好應淘汰。
區分度的計算方法有兩種：區分度指數和相關係數。
區分度指數
區分度指數（index of discrimination，D）的具體公式如下：
式中，D為區分度指數，PH為高分組的項目難度，PL為低分組的項目難度。
顯而易見，高低分兩組越是極端，區分度指數就越明顯。但個案過少則會減少結果的信度。凱利（T. L. Kelley）指出，在常態分配中，兼顧兩者的最佳百分數是27%。對於小樣本，如一個常規教學班，可取25%-33%之間的任何數字，只要使用方便。
區分度指數D和項目難度P彼此並不獨立，項目難度為中等水平時，區分度指數為最大值。不同難度的項目的區分度指數最大值見表1-2。
PT | PH | PL | D最大值 |
1.00 | 1.00 | 1.00 | 0.00 |
0.90 | 1.00 | 0.80 | 0.20 |
0.80 | 1.00 | 0.60 | 0.40 |
0.70 | 1.00 | 0.40 | 0.60 |
0.60 | 1.00 | 0.20 | 0.80 |
0.50 | 1.00 | 0.00 | 1.00 |
0.40 | 0.80 | 0.00 | 0.00 |
0.30 | 0.60 | 0.00 | 0.60 |
0.20 | 0.40 | 0.00 | 0.40 |
0.10 | 0.20 | 0.00 | 0.20 |
0.00 | 0.00 | 0.00 | 0.00 |
相關係數法
通過計算某一題目得分與測驗總得分或效標分數的相關係數來判定。相關越大，區分度越高。
1）點二列相關
當測驗總分為正態連續變數，題目分為二分變數（對、錯或通過、未通過）時，可用點二列相關公式計算區分度。其計算公式是：
2）二列相關法
測驗總分與題目分兩列變數都是正態連續變數，但其中一列變數由於某種原因被分為兩個類別，可以用二列相關法計算題目區分度。其計算公式是：
式中，rb為二列相關係數，即題目區分度；
為答對題目被試測驗總分平均分，
為答錯題目被試測驗總分平均分，st為全體被試測驗總分標準差，p為答對題目被試占總被試人數比率，q=1-p，y為正態曲線中答對比例所在位置曲線高度。
二列相關係數rb的顯著性用下列公式：
式中，rb為二列相關係數，p為答對題目被試占總被試人數比率，q=1-p，y為正態曲線中答對比例所在位置曲線高度。求出Z值後，查正態曲線表，若Z>1.96，則相關顯著。
3）四分相關法
四分相關法適用於兩列變數都是正態連續變數，但都要人為地一分為二的統計資料。計算這類相關採用皮爾遜餘弦π公式，所得相關為四分相關係數，公式如下：
式中，A、B、C、D分別代表四個類別。A和D代表相同符號的次數（++或--），B和C代表相反符號的次數（+-或-+）。
四分相關係數是否顯著，可通過下式檢驗：
式中，p1、q1、p2、q2為每個類別的累積百分比，y1和y2分別是累計百分比為p1、p2時正態曲線的高度，可以通過查常態分配表得到。
運用四分相關計算題目區分度時，樣本容量應在200以上，計算出的結果才能比較好地說明問題。
4）
相關法
檢驗
的顯著性水平套用下式：
求得X2值以後，查X2表，看X2值是否達到顯著性水平。若X2值顯著，則值也顯著。
5）積差相關法
對於心理測驗中的多值評分的題目和學科測驗中的主觀性試題，可以用積差相關法計算題目分和測驗總分的相關係數，作為題目區分度值。
6）題目與總分相關重疊的校正
計算題目分與測驗總分的相關，這是一種局部和總體的相關。在由題目分與總分計算出的相關係數中，必然有相關重疊的成分，使相關係數即題目的區分度偏高，以致各個題目所貢獻的變異數比例都很小時，才能把題目與總分相關作為題目區分度的指標。假如不具備這些條件，需要用校正公式對計算出來的相關係數作校正，以去除相關重疊的成分。校正公式如下：
一般而言，當測驗題目數量較少，且題目與總分相關不高時，需要用上式對計算出的題目區分度作校正；若一份測驗有20個以上的題目時，則不需作校正。
項目特徵曲線
區分度和難度
難度和區分度都是相對的，是針對一定團體而言的（絕對的難度和區分度是不存在的）。一般說來，較難的項目對高水平的被試區分度高，較易的項目對水平低的被試區分度高，中等難度的項目對中等水平的被試區分度高。這與中等難度的項目區分度最高的說法並不矛盾，因為對被試總體是較難或較易的項目，對水平高或水平低的被試便成了中等難度。由於人的多數心理特徵呈常態分配，所以當需要把人作最大程度區分時，項目難度的分布也以正態為好，即特別難與特別容易的題目較少，接近中等難度的題目較多，而所有題目的平均難度為0.50。
什麼情況下區分度高呢？或者說什麼樣的題目才能最大限度地區分不同水平的人群？這就引出了試題項目評價的第二個指標：難度。題目的難度過高，很少人能答對，大部分得分都很低；難度過低，很少人會答錯，分數分布在高分端。因而過難或過易的題目都不能很好地區分不同水平的個體。因而當題目的難度為中等時，區分度最高。
一個好的測驗中是不是要求所有題目都是中等難度？那高考、研究生入學考試這樣的高水平測試為何還有難度很大或很小的題目？這是因為在一個測驗中如果都是中等難度的題目，就又走向另一個極端，即對中等程度的人有最佳鑑別力，而對水平高和水平低的那部分人不能做很好的區分。簡言之，不同難度的題目對於不同水平的人來說區分度是不同的。鑒於全體受測者的能力分布往往是呈正態的，測驗中題目難度的分布也基本為常態分配，即難、中、易都有分布，中等難度題目最多。只有這樣才能保證整個測驗有較高的鑑別力。
