物體振動時的粘彈性稱為動粘彈性。同時把單方向的應力一變形所表現的粘彈性,稱為靜粘彈性。對於單方向作用,即使應力一定,變形也會增大,容易使物體的內容結構發生變化從而難於測定其粘彈性,對粘彈性體採用動態測定法,如共振法或脈衝法。
基本介紹
- 中文名:動粘彈性
- 外文名:Dynamic viscoelastic
- 釋義:物體振動時的粘彈性
- 靜粘彈性:單方向的應力一變形
- 測定:共振法或脈衝法
- 表示方法:動粘彈性係數
動粘彈性的測定
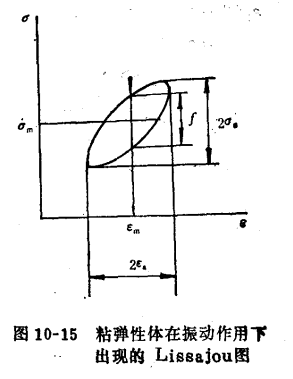 圖1
圖1 圖2
圖2
物體振動時的粘彈性稱為動粘彈性。同時把單方向的應力一變形所表現的粘彈性,稱為靜粘彈性。對於單方向作用,即使應力一定,變形也會增大,容易使物體的內容結構發生變化從而難於測定其粘彈性,對粘彈性體採用動態測定法,如共振法或脈衝法。
 圖1
圖1 圖2
圖2物體振動時的粘彈性稱為動粘彈性。同時把單方向的應力一變形所表現的粘彈性,稱為靜粘彈性。對於單方向作用,即使應力一定,變形也會增大,容易使物體的內容結構發生...
viscoelasticity 流體的粘滯性及彈性的綜合性質。粘彈性聚合物在加工過程中通常是從固體變為液體(熔融和流動),再從液體變固體(冷卻和硬化),所以加工過程中聚合物於...
粘彈性理論簡介 固體力學的一個研究內容。它在考慮材料的彈性性質和粘性性質的基礎上,研究材料內部應力和應變的分布規律以及它們和外力之間關係。材料的粘性性質主要...
用靜態測定法揭示的物體的粘彈性稱靜粘彈性,如拉伸(壓縮)試驗所測的彈性率、蠕變性質的滯後時間、蠕變柔量、鬆弛彈性的應力鬆弛時間等。...
食品的粘彈性是指食品材料受力作用時既表現出彈性又表現出粘性的一種特性。在受到力的作用時,食品可以發生明顯的變形,當外力撤去後一部分能量會被儲存起來,而另一...
高聚物的粘彈性viseoelastieityofpolymers 同一高聚物可以呈現彈性固體到粘性液體之間的各種性能,是高聚物力學性能的重要特性。一個理想的彈性固體具有確定的形狀,在外力...
同時具有彈性和粘性兩種不同機理的形變,綜合地體現為粘性流體和彈性固體兩者的特性的材料稱為粘彈性體。粘彈性體材料受力後的變形過程是一個隨時間變化的過程,卸載...
《粘彈性結構的動力學分析》是蘭州大學丁睿發表的論文,由朱正佑、程昌鈞指導。...... 《粘彈性結構的動力學分析》是蘭州大學丁睿發表的論文,由朱正佑、程昌鈞指導...
土體在骨架應力作用下,顆粒的重新排列和骨架的錯動具有明顯的時間效應,土體的變形和內部應力變化都與時間有關,通過大量的試驗證明了土體具有粘彈性特徵。土體的粘彈...
線性粘彈性模型是由線性的粘性元件和彈性元件並聯而成的一種力學計算模型,屬於流變學理論,主要用於土(動)力學的相關研究。...
粘彈性流體,介於黏性流體和彈性固體之間。它們同時表現出黏性和彈性,在不超過屈服強度的條件下,剪應力除去以後,其變形能部分的復原。屬於此種流體的有麵粉團、凝固...
《瀝青混合料粘彈性力學及材料學原理》是由人民交通出版社於2006-3出版的圖書,作者劉立新。...
靜態粘彈性指蠕變和鬆弛現象,高聚物在室溫下已有明顯的蠕變和鬆弛現象。鬆弛過程高分子聚合物的應力鬆弛 (stress relaxation)就是在固定的溫度和形變下,聚合物內部的...
復模量模型又分為復常數模量和頻變復模量模型,是分析粘彈性材料結構動力學回響...比如黃潤秋等人在對隧址區山體的地震動作用特點進行研究的過程中,採用復模量模型...
