力系的簡化與平衡

用一個等效的簡單力系來代替作用在剛體上的複雜力系稱為力系的簡化；如果作用在剛體上的力系滿足平衡條件，此時力系不改變剛體的原有運動狀態，則稱為力系的平衡。

基本介紹

• 中文名：力系的簡化與平衡
• 外文名：The simplification and balance of the force system
• 領域：力學
• 內容：力系的簡化、力系的平衡
• 作用對象：剛體
• 作用效果：不改變剛體的原有運動狀態

基本概念

用一個等效的簡單力系來代替作用在剛體上的複雜力系稱為力系的簡化；如果作用在剛體上的力系滿足平衡條件，此時力系不改變剛體的原有運動狀態，則稱為力系的平衡。

力系的簡化

定義

一個力系對剛體的作用效果，可以用另一個力系等效。這個過程稱為力系的簡化。

力的平移定理

將作用於剛體上的力F 平移（大小、方向不變）至同一剛體上且不在力F作用線上的其他點而保證F作用效果不變，則必須增加一個附加力偶。其力偶矩 M 等於原力F對平移點之矩。

力系的平移定理——力系可以簡化的基礎；

一般力系向一定點的簡化

一個一般力系由作用於剛體上Di 點的力Fi （i =1，2，… n）組成。O為剛體上任意確定點。根據力的平移定理和力的可傳遞性，將力系中各力向O點平移，得到一個匯交於O的匯交力系Fi ，和一個力偶系Mi。

其中，

根據力系和力偶系的合成，最終的簡化結果為過O點的一個力Fo

以及一個力偶

力系向一點簡化後的主矢和主矩在坐標軸上的投影

力系簡化結果總結

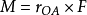
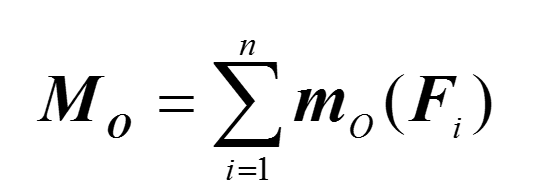
1. Fr=0；M0=0力系平衡
   
2. Fr=0；M0≠0力系簡化為一個合力偶，力偶矩為Mo
   
3. Fr≠0；M0=0力系與一個力等效：該力過簡化中心O，大小、方向與力系的主矢相同。
   
4. Fr≠0；M0≠0
   （1）Fr·M0=0簡化為一個合力
   （2）Fr×M0=0中心線過簡化中心O的力螺旋
   （3）Fr×M0≠0中心軸過B點的力螺旋
   

力系的平衡

一般力系的平衡條件

力系幾何平衡條件 ：

由 向直角坐標軸投影，即空間力系平衡方程基本形式。

特殊力系的平衡方程

由基本式去掉力系幾何性質自動滿足的方程：

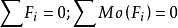
其他相關內容

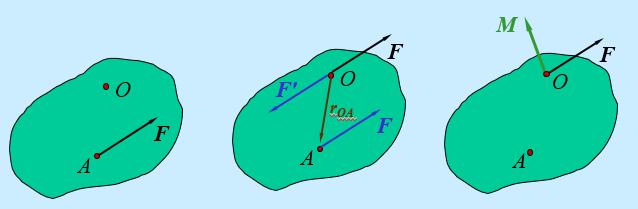
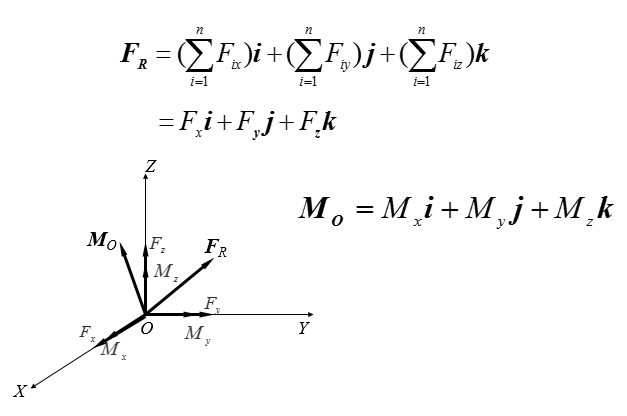
任何一個作用在剛體上給定點A上的力F（圖1）可以等效於作用在另一點B的一個力F'(F'=F)和一個附加力偶(即F和-F'組成的力偶)，此力偶的力偶矩矢量等於作用在點A的力F對於點B之矩。即力F同{F'，M=_r×F'} 等效，式中F為點A對點B的矢徑。如果在剛體上作用著任意分布的力系{F₁,F₂,…,F_n}(圖2), 為了簡化此力系，可在剛體上任取一個點O，稱為簡化中心，將力系中的每一個力F_i平行移動至簡化中心O，為了保持力的等效性，需增加一個附加力偶，它的力偶矩矢量為M_Oi=M_O(F_i=_ri×F_i,式中_ri是力F_i的作用點A_i對於點O的矢徑。把這n個平移後的力在點O相加，得到一個合矢量，稱為力系的主矢量。把n個附加力偶進行合成，得到一個力偶，

稱為力系對點O的主矩。力系的主矢量R和力系對於點O的主矩M_O是力系的兩個基本物理量。由F和M_O所構成的力系 {R，M_O}同原力系{F₁,F)₂,…,F_n}等效。主矢量R不隨所選取的簡化中心O的位置而變,但主矩卻依賴於簡化中心的選取。如對點O的主矩為M_O，則對剛體上另一點O'的主矩limu（x）=0，式中R表示由點O'到點O的矢徑。

如果一個給定的空間力系向某點O簡化時得到的主矢量h≠0，而主矩M_O=0，則該力系同一個力等效，此力稱為力系的合力，它的作用線通過點O，其大小和方向與主矢量F相同。如果力系向點O簡化時，得到的主矢量R=0，而主矩M_O0,則該力系同一個力偶等效，此力偶稱為力系的合力偶，它的力偶矩矢量等於主矩M_O。如果力系向點O簡化時得到的主矢量R同主矩M_O平行，則力系同一個力螺旋等效,這時主矢量R的作用線稱為力螺旋軸。
如果力系中各力的作用線都位於同一個平面，則稱此力係為平面力系。如果力系中各力的作用線都同空間某一直線平行，則稱此力係為平行力系。對於這兩種力系，簡化的結果或者是一個力或者是一個力偶。如果力系中各力的作用線相交於一點O，則稱力係為匯交力系，它和通過點O的一個力等效。如果力系是由n個力偶所組成的,則稱它為力偶系,它同一個力偶等效。如果作用在剛體上的力系向剛體上任意一點O簡化時,它的主矢量R和主矩M_O同時為零,則稱此力係為平衡力系。R=0,M_O=0稱為力系的平衡條件。