力學系統平衡的穩定性是指處於平衡位置的某一力學系統,在受到外力系的微小擾動後,仍能繼續處於平衡位置的性質。
力學系統平衡的穩定性力學系統平衡的穩定性平衡位置系統的穩定性定義 考慮個自由度的完整系統(見約束),它的位置由個廣義坐標(,,…,)來確定。一個力學系統有幾個平衡位置,可進行坐標變換,使這個所要討論的平衡位置就是坐標系的原點,於是對這平衡位置有:
 力學系統平衡的穩定性
力學系統平衡的穩定性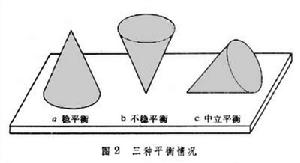 力學系統平衡的穩定性
力學系統平衡的穩定性若在時間=有一擾動,使系統位形產生偏差及。如果對於任何ε>0可找出δ=δ()>0,使成立,那么對於一切>有不等式,則稱這系統在這位置是穩定的,否則稱為不穩定。1788年J.L.拉格朗日發表下列定理:如果一個保守系統的勢能在某個平衡位置是個孤立的極小值,那么這系統在這平衡位置是穩定的(這個定理後來被P.G.L.狄利克雷所證明)。1892年Α.М.里雅普諾夫得到上述定理的一部分逆定理。若保守完整系統的勢能在某平衡位置上是個極大值,則這平衡不穩定。H.Γ.切塔耶夫把上述定理加以擴充為: 若保守系統的勢能在某平衡位置無極小值,則在這位置的平衡是不穩定的。對於非保守系統,如果這系統是在一個保守系統的基礎上再附加一個迴轉儀力而成的,那么上述拉格朗日定理依舊成立,因為迴轉儀力對系統不做功。若附加了耗散力,則使系統的機械能不斷減少,於是這系統的哈密頓函式對時間的變化率夑不為正。對於 夑為負定函式,而為正定的情況,拉格朗日定理依舊成立。
彈性系統的平衡穩定性 工程上的所有結構都不是絕對剛體,因而要考慮強度和剛度問題就必須要研究應力和應變。對於有特殊結構和尺寸的構件,當受力大到某臨界值時,便發生失穩現象,產生較大的有限變形,結構會受到嚴重破壞並造成事故,例如:①受壓桿件。對於桿件受拉力和長度較短的受壓桿件,除非達到強度極限的破壞現象,否則系統總是穩定的。但是,對於細長桿的兩端受到軸向壓力時,當壓力超過臨界力時便發生失穩現象──桿彎成撓曲狀。對於像靜定桁架那樣的結構,如果存在著這樣的壓桿,就像少了一根桿,以致結構變成幾何可變系統而損壞。所以這問題對建築結構和鐵路橋樑的設計是很重要的。②受外壓的薄壁容器。化工廠中內壓較大的薄壁容器的損壞一般是強度不夠的問題。但是,對於外壓大於內壓的薄壁容器,當它的壓力差超過臨界壓力時,便會發生失穩。如薄壁圓筒在筒長和筒徑的比例不當時,筒壁就有可能發生各種不同形式的凹陷而造成破壞。
 力學系統平衡的穩定性
力學系統平衡的穩定性 力學系統平衡的穩定性
力學系統平衡的穩定性 力學系統平衡的穩定性
力學系統平衡的穩定性 力學系統平衡的穩定性
力學系統平衡的穩定性