劃分幾何

劃分幾何(partition geometry)是一類組合幾何，它是由有限集E上的劃分導出的組合幾何，在劃分幾何中，點與線的共線關係由劃分之間的精細關係決定。

基本介紹

• 中文名：劃分幾何
• 外文名：partition geometry
• 所屬學科：數學
• 所屬問題：組合序
• 簡介：有限集E上的劃分導出的組合幾何

基本介紹

劃分幾何是由有限集E上的劃分導出的組合幾何。設|E|=n，劃分π包含有k個劃分塊，記π的秩r(π)=n-k，因此，劃分π為劃分幾何的一個點，若且唯若π的最大劃分塊惟一且僅含兩個元素，例如，n=4，π₁=(ab)(c)(d)，π₂=(a) (bc)(d)均為點。此時，簡記π₁=(ab)，π₂=(bc)，而劃分π為線，既可為π₃=(abc)(d)，也可為π₄=(ab)(cd)等。

在劃分幾何中，點與線的共線關係由劃分之間的精細關係決定。例如，π₁，π₂均為π₃的精細劃分，所以，π₁和π₂這兩點均線上π₃之上，其他如圖所示，E的元素可由劃分π建立等價關係(π)，a(π)b若且唯若a，b同屬π的一個劃分塊。對於任意劃分a和π均可建立格的結運算和交運算，a(π∨σ)b若且唯若有元素u₀=a，u₁，u₂，…，u_t=b，使得對所有的0≤i≤t有u_i(π)u_i+1或u_i(σ)u_i+1；a(π∧σ)b若且唯若a(π)b且a(σ)b，從而，由劃分幾何導致格。

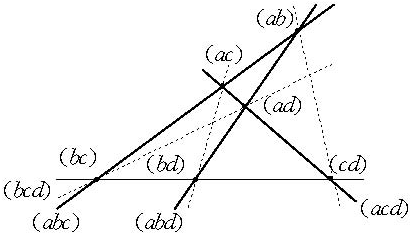圖1

相關介紹

組合幾何是一種組合構形，它是既不含自環也不含平行元素的擬陣M(E)，這樣的擬陣亦稱簡單擬陣，從M(E)上的閉包運算元看，組合幾何為滿足下述條件的擬陣：

1.空集∅的閉包.

2.對於E的任意元素e，有.

組合幾何的點、線、面等分別為秩為1，2，3的平集，上點、上線、上面則分別為上秩為1，2，3的平集，特別地，上點又稱為組合幾何的超平面，組合幾何關切的點、線、面這些基本要素的關係是由集合包容關係導出的序關係，一種特殊的關聯關係，例如，一個點是否在一條線中，一條線是否在一個面中等，其背景在具體意義上可以差別極大，既可以是集合劃分之間的精細關係，也可以是連通圖上邊集構成的圈的關係，當組合幾何的維數較低時，可以把其點、線、面等要素之間的關聯關係一一對應於投影空間上點集的線性相關性，從而使得組合幾何具有明顯的直觀性。

考慮在投影平面S上的點a，b，c，d，e，f組成的點集E，其中{a，e，f}，{a，b，c}，{b，d，f}，{c，d，e}共線如下圖所示，S中平集的秩為決定該平集的最少點數，因此，此組合幾何G(E)的平集可由S上的平集F與E的交集F∩E給出，{a}，{b}，{c}，{d}，{e}，{f}為第一類平集，{a，b，c}，{c，d，e}，{b，d，f}，{a，e，f}，{a，d}，{c，f}，{b，e}為第二類平集，它們的秩由滿足F∩A=A的投影空間上的平集F的秩給出，因此，第一類平集的秩為1，這樣它們是G(E)中的點；而第二類平集的秩為2，它們為G(E)中的線，儘管平集{a，d}，{b，e}，{e，f}中並沒有聯線，這是組合幾何與投影幾何的不盡相同之處。

圖2