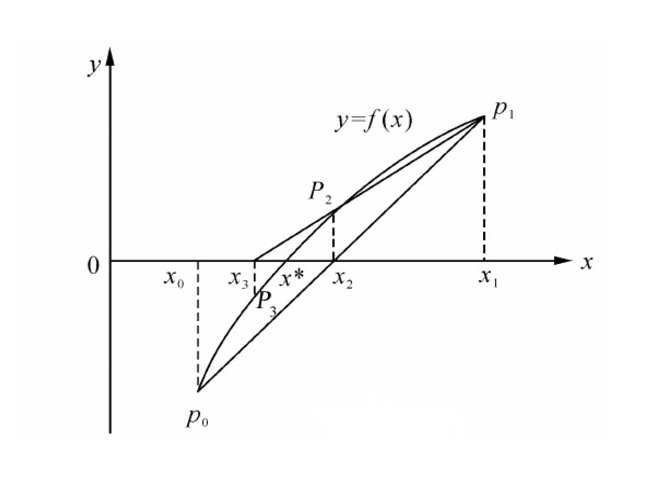
割線法,又稱弦割法、弦法,是基於牛頓法的一種改進,基本思想是用弦的斜率近似代替目標函式的切線斜率,並用割線與橫軸交點的橫坐標作為方程式的根的近似。它是求解非線性方程的根的一種方法,屬於逐點線性化方法。
基本介紹
- 中文名:割線法
- 外文名:Secant method
- 又稱:弦割法、弦法
- 學科:數學
- 用來:求解非線性方程的解
- 屬於:逐點線性化方法
定義,割線,割線法,割線法收斂定理,算法描述,例題,
定義
割線
給定函式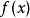 上兩點
上兩點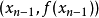 和
和 ,這兩點所在直線即為割線,方程為:
,這兩點所在直線即為割線,方程為:
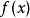
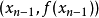

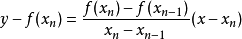
割線法
給定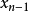 和
和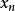 ,通過點
,通過點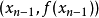 和
和 的割線,設
的割線,設 為這條割線與x軸的交點的橫坐標,故,令
為這條割線與x軸的交點的橫坐標,故,令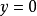 ,則
,則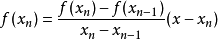
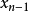
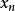
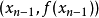


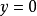
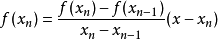
其中,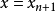 為該方程的解。
為該方程的解。
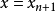
解方程,得:
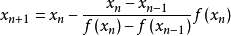
割線法收斂定理
設 ,
,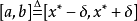 ,
,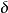 為足夠小的正數,
為足夠小的正數,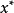 是
是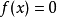 的根,如果
的根,如果

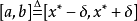
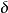
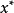
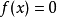
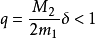
其中,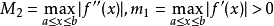 ,則由
,則由
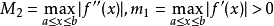
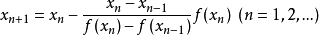
確定的序列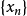 以
以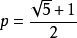 的速度收斂到
的速度收斂到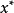
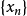
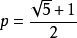
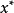
算法描述
割線法的算法描述如下:
輸入:

輸出: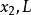
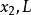
(1)

(2)while 

(a)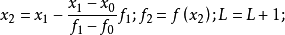
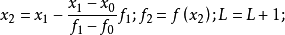
(b)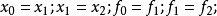
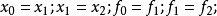
(c) if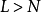 then
then
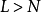
輸出信息失敗,停止運算
endif;
(3)endwhile;
例題
用割線法求方程 在區間
在區間 內的實根。
內的實根。


解:取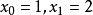 ,代入公式
,代入公式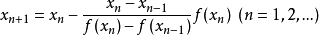
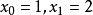
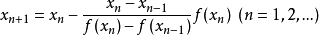
得到: