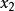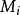針對傳統歐幾里得距離存在的問題，切面距離算法假設待分類的樣本和處於同一個流形上的樣本具有相同的類別，根據鄰近流形關於聚集機率的知識導出距離度量，是一種非參數的最近鄰算法。
基本介紹
- 中文名：切面距離算法
- 外文名：tangent distance algorithm
- 基礎：流形假設
- 性質：局部性；非參數
- 學科：計算機視覺
- 套用：人工智慧
問題提出,切面距離,細節,
問題提出
在模式識別中，一種簡單但效率低下的方法是使用簡單的距離測量，例如表示原始輸入矢量之間的歐幾里德距離。這種方法效率很低，因為幾乎所有類別的實例都必須存在於原型集中，例如，在手寫數字識別中，必須存儲所有可能出現位置、大小、角度、書寫樣式、線條粗細和傾斜的每個類的數字。在實際情況中，這種方法導致不切實際的原型集或普通的識別準確性。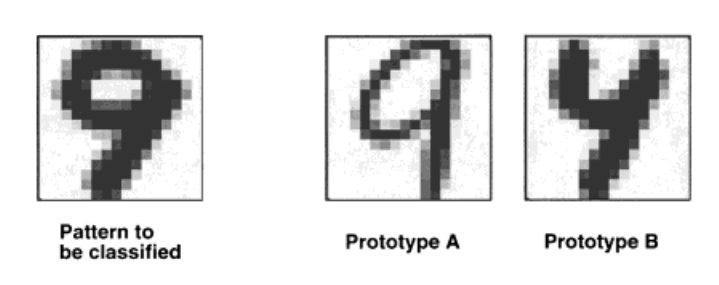
圖1
圖1如圖1，一個寬線條的、傾斜的“9”的待標記圖像必須通過從兩個圖像中找到最接近的原型圖像來分類，這兩個圖像分別代表一個線條細的、直立的“9”和一個線條粗的、傾斜的“4”。根據歐幾里德距離，“4”和待標記圖像更接近，但卻不是正確的分類。
處理這類問題的經典方法是使用特徵提取器，其目的是計算模式的特徵表示，對於字元識別，特徵表示應在位置，尺寸變化，輕微旋轉，扭曲或線條厚度變化方面不變。特徵提取器的設計和實現是構建模式識別系統的主要瓶頸。
另一種方法是使用不變距離測量，以這種方式構造原型和模式之間的距離不受模式或原型的無關變換的影響。 通過不變距離測量，每個原型可以匹配許多可能的模式實例，從而大大減少了所需的原型數量。其關鍵思想是構建一個距離度量，該度量對於某些選定的變換（例如平移，旋轉等）是不變的。
切面距離
切面距離算法包括計算非線性流形
和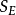
的最佳近似線性表面之間的最小距離。它主要解決了三個問題：
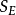
(1) 線性流形具有簡單的解析表達式，可以很容易地計算和存儲；
(2) 找到線性流形之間的最小距離是一個可以有效求解的簡單最小二乘問題；
(3) 這個距離是局部的，而不是全局的、不變的。
因此，“6”和稍旋轉的“6”之間的距離很小，但“6”和“9”之間的距離很大。P和E之間的不同距離示意圖如圖2。
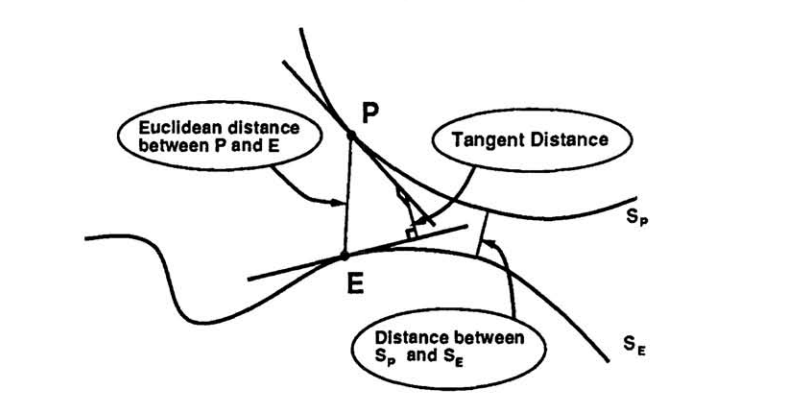圖2P和E的歐幾里得距離和切面距離
