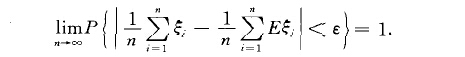
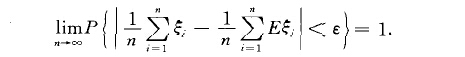
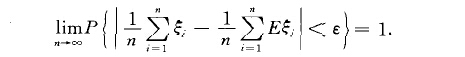
大數律,即大數定律,是機率論中討論隨機變數序列的算術平均值向常數收斂的定律,是機率論與數理統計學的基本定律之一。大數律有弱大數律和強大數律之分。在隨機...
切比雪夫大數定律是數學學科機率論裡面一個重要的定律。...... 切比雪夫大數定律是數學學科機率論裡面一個重要的定律。設隨機變數序列 兩兩不相關,且期望存在 ,方...
馬爾可夫大數律(Markov law of large num-hers)一種弱大數律.設隨機變數序列y } }z }…滿足條件:對於任意n)l,均有馬爾可夫大數律不僅能用於獨立的隨機變數...
該定律是切比雪夫大數定律的特例,其含義是,當n足夠大時,事件A出現的頻率將...只需要用到倒向鞅的知識和Hewitt-Savage 0-1律,不過這也是現代機率論的知識。...
伯努利大數律(Bernoulli law of large num -hers)關於伯努利試驗的弱大數律.設產,是n重伯努利試驗中事件A出現的次數,而p(0<p<1)是每次試驗中事件A出現的...
設X是一個隨機變數取取區間(0,∞)上的值,F(x)是它的分布函式,設Xα(α >0)的數學期望M(Xα )存在,a>0,則不等式成立。這叫做切比雪夫定理,或者切...
這時稱傳n}服從馬爾可夫大數定律.馬爾可夫(M2,pKOB } A. A.)認真研究了切比雪夫大數定律,並利用切比雪夫不等式給出了此定律的證明....
切比雪夫的工作為數論研究開闢了新方向。 在機率論方面,切比雪夫建立了證明極限定理的新方法──矩法,用十分初等的方法證明了一般形式的大數律,研究了獨立隨機變數...
切比雪夫函式(Chebyshev function)重要的數論函式之一。它是切比雪夫(Чебышев,П.Л.)為了證明素數定理而給出的。使函式Ψ(x)與對數函式建立了簡單的...
近代極限理論——無窮可分分布律的研究也經C.H.伯恩斯坦(Бернштейн)、A.Я.辛欽(Хинчин)等人之手而臻於完善,成為切比雪夫所開拓的古典極限...
近代極限理論——無窮可分分布律的研究也經C.H.伯恩斯坦(Бернштейн)、A.Я.辛欽(Хинчин)等人之手而臻於完善,成為切比雪夫所開拓的古典極限...
在機率論中,他發展了矩法,擴大了大數律和中心極限定理的套用範圍。馬爾可夫最...後來在機率論的研究中,馬爾科夫一再回到矩的問題上來,並對切比雪夫的矩問題作...
極限定理大數定律 定理1(切比雪夫定理的特殊情況)設隨機變數 相互獨立,且具有...只需要用到倒向鞅的知識和Hewitt-Savage 0-1律,不過這也是現代機率論的知識。...
2.了解切比雪夫大數定律、伯努利大數定律和辛欽大數定律(獨立同分布隨機變數序列的大數定律) .3.了解棣莫弗-拉普拉斯定理(二項分布以常態分配為極限分布)和列維...
第四章 大數定律 §1切比雪夫不等式 §2中心極限定理 §3大數定律 第五章 參數估計和假設檢驗 §1抽樣分布 §2點估計 §3區間估計 §4假設檢驗 §5正態總...
大數定律和中心極限定理考試內容:切比雪夫(Chebyshev)不等式 切比雪夫大數定律 伯努利(Bernoulli)大數定律 辛欽(Khinchine)大數定律 棣莫弗-拉普拉斯(De Moivre-...
2.1.2 離散型分布變數及其分布律2.1.3 0-1分布與二項分布...5.2.2 獨立同分布隨機變數序列的切比雪夫大數定律§5.3 中心極限定理...
大數法則是對於大量的隨機現象(事件),由於偶然性相互抵消所呈現的必然數量規律的一系列定理的統稱。常見的有三個大數法則:切比雪夫(Chehyshev)大數法則...
19世紀末,俄國數學家切比雪夫、馬爾可夫、李亞普諾夫等人用分析方法建立了大數...且隨著試驗次數n的增加,其擺動的幅度越來越小,則稱數p為隨機事件A的機率,記...
1.了解向量的概念,掌握向量的加法和數乘運算法則.2.理解向量的線性組合與線性...3.了解切比雪夫不等式.大數定律和中心極限定理考試要求1.了解切比雪夫大數定律...
第五章:大數定律和中心極限定理考試內容切比雪夫(Chebyshev)不等式切比雪夫大數定律伯努利(Bernoulli)大數定律辛欽(Khinchine)大數定律 棣莫弗-拉普拉斯(De Moivre-...
2.2.1分布律與分布函式 292.2.2常用的離散型分布 322.3連續型隨機變數 ...4.4.1切比雪夫不等式 934.4.2大數定律 944.4.3中心極限定理 97...
切比雪夫(Chehyshev)大數法則貝努里(Bermulli)大數法則泊松(Poisson)大數法則保險精算精算師 保險業的發展離不開精算師,隨著保險業的發展,嚴密的數學基礎建立,...
第一節 引言第二節 切比雪夫不等式第三節 大數定律第四節 中心極限定理本章小結思考與訓練(六)課外閱讀第七章 抽樣分布第一節 引例第二節 總體與樣本...
大數定律與中心極限定理、數理統計的基本概念、參數估計、假設檢驗、回歸分析與...5 大數定律與中心極限定理 5.1 切比雪夫不等式 5.2 大數定律 5.3 中心...
第二節 離散型隨機變數及其分布律第三節 連續型隨機變數及其機率密度第四節 ...第一節 切比雪夫不等式第二節 大數定律第三節 中心極限定理本章知識結構及...
1.離散型隨機變數的分布律和分布函式2.連續型隨機變數的密度函式和分布函式...1.切比雪夫不等式2.大數定律3.中心極限定理二、習題分類、解題方法和示例...
