基本介紹
研究歷史,研究內容,設計分析,設計原則,AES徵集,算法要求,分組長度足夠大,密鑰量足夠大,密碼變換足夠複雜,技術總結,優點,缺點,
研究歷史
現代分組密碼的研究始於20世紀70年代中期，至今已有40餘年歷史，這期間人們在這一研究領域已經取得了豐碩的研究成果。
對於分組密碼，在早期的研究，基本上是圍繞DES進行的，推出了一些類似的算法，例如：LOKI，FEAL，GOST等。進入20世紀90年代，人們對DES算法研究更加深入，特別是差分密碼分析（differential cryptanalysis）和線性密碼分析（linear cryptanalysis）的提出，迫使人們不得不研究新的密碼結構。IDEA密碼打破了DES類密碼的壟斷局面，隨後出現了SQUARE、SHARK、SAFER-64等採用了結構非常清晰的代替—置換（SP）網路，每一輪由混淆層和擴散層組成，從理論上給出了最大差分特徵機率和最佳線性逼近優勢的界，證明了密碼對差分密碼分析和線性密碼分析的安全性。
1997年-2000年，AES的徵集掀起了分組密碼研究的新高潮，15個AES候選算法反映了當前分組密碼設計的水平，也可以說是近幾年研究成果的一個匯總。
目前分組密碼所採用的整體結構可分為Feistel結構（例如CAST—256、DEAL、DFC、E2等）、SP網路（例如Safer+、Serpent等）及其他密碼結構（例如Frog和HPC）。加解密相似是Feistel型密碼的一個實現優點，但它在密碼的擴散似乎有些慢，例如需要兩輪才能改變輸入的每一個比特。SP的網路結構非常清晰，S被稱為混淆層（非線性層），主要起混淆作用。P被稱為擴散層，主要起擴散作用。在明確S和P的某些密碼指標後，設計者能估計SP型密碼抵抗差分密碼分析和線性密碼分析的能力。SP網路和Feistel網路相比，可以得到更快速的擴散，但是SP密碼的加/解密通常不相似。
分組密碼是現代密碼學中的一個重要研究分支，其誕生和發展有著廣泛的實用背景和重要的理論價值。目前這一領域還有許多理論和實際問題有待繼續研究和完善。這些問題包括：如何設計可證明安全的密碼算法；如何加強現有算法及其工作模式的安全性；如何測試密碼算法的安全性；如何設計安全的密碼組件，例如S—盒、擴散層及密鑰擴散算法等。
研究內容
大體上，分組密碼的研究包括三方面：分組密碼的設計原理，分組密碼的安全性分析和分組密碼的統計性能測試。
設計分析
分組密碼的設計與分析是兩個既相互對立又相互依存的研究方向，正是由於這種對立促進了分組密碼的飛速發展。早期的研究基本上是圍繞DES進行，推出了許多類似於DES的密碼，例如，LOKI、FEAL、GOST等。進入90年代，人們對DES類密碼的研究更加深入，特別是差分密碼分析（differential cryptanalysis）和線性密碼分析（linear cryptanalysis）的提出，迫使人們不得不研究新的密碼結構。IDEA密碼的出現打破了DES類密碼的壟斷局面，IDEA密碼的設計思想是混合使用來自不同代數群中的運算。隨後出現的Square、Shark和Safer-64都採用了結構非常清晰的代替-置換（SP）網路，每一輪由混淆層和擴散層組成。這種結構的最大優點是能夠從理論上給出最大差分特徵機率和最佳線性逼近優勢的界，也就是密碼對差分密碼分析和線性密碼分析是可證明安全的。
設計原則
擴散（diffusion）和擾亂（confusion）是影響密碼安全的主要因素。擴散的目的是讓明文中的單個數字影響密文中的多個數字，從而使明文的統計特徵在密文中消失，相當於明文的統計結構被擴散。例如，最簡單的方法讓明文中的一個數字影響密文中的k個數字，可以用：
擾亂是指讓密鑰與密文的統計信息之間的關係變得複雜，從而增加通過統計方法進行攻擊的難度。擾亂可以通過各種代換算法實現。
設計安全的分組加密算法，需要考慮對現有密碼分析方法的抵抗，如差分分析、線性分析等，還需要考慮密碼安全強度的穩定性。此外，用軟體實現的分組加密要保證每個組的長度適合軟體編程（如8、16、32……），儘量避免位置換操作，以及使用加法、乘法、移位等處理器提供的標準指令；從硬體實現的角度，加密和解密要在同一個器件上都可以實現，即加密解密硬體實現的相似性。
AES徵集
AES的徵集掀起了分組密碼研究的新高潮，15個AES候選算法反映了當前分組密碼設計的水平，可以說是近幾年研究成果的一個總匯。分組密碼所採用的整體結構可分為Feistel結構（如CAST-256、DEAL、DFC/E2等）、SP網路（如Safer+、Serpent等）及其他密碼結構（如Frog和HPC）。Feistel結構由於DES的公布而廣為人知，已被許多分組密碼所採用。Feistel結構的最大優點是容易保證加解密相似，這一點在實現中尤其重要。而SP網路比較難做到這一點，但是SP網路的擴散特性比較好。在現有的分組密碼中，所有的基本運算有異或、加、減、查表、乘及數據依賴循環等。查表運算提供了DES的安全基礎，仔細地選擇S-盒能較好地抗擊線性和差分密碼分析，提供好的數據及密鑰比特的雪崩特性。不過，S-盒需要一些存儲器，所以S-盒的規模不能太大。15個AES候選算法所採用的S-盒規模有6種，分別是4×4、8×8、8×32、11×8、13×8、及8×32。S-盒的另一中稱呼是黑盒子，它常給人造成故意設定陷阱的嫌疑，因此，Safer+等選取公開的數學函式，避免嫌疑。S-盒的設計與分析是分組密碼設計中的重要環節，它的好壞直接影響密碼體制的安全性，對S-盒的設計並沒有一個完備的要求，但總的希望是增強S-盒的非線性度、差分均勻性及分量函式的代數次數和項數。
對分組密碼安全性的討論主要包括差分密碼分析、線性密碼分析和強力攻擊等。從理論上講，差分密碼分析和線性密碼分析是目前攻擊分組密碼的最有效的方法，而從實際上說，強力攻擊是攻擊分組密碼最可靠的方法。到目前為止，已有大量文獻討論各種分組密碼的安全性。自AES候選算法公布以後，國內外許多專家都致力於候選算法的安全性分析，預計將會推出一些新的攻擊方法，這無疑將進一步推動分組密碼的發展。
設明文m與密文c均為二進制0、1數字序列，它們的每一個分量mi，DF(2)(i=0，1，2，…，n-1)，則明文空間為{0，1，…，2n-1}，密文空間也為0，1，…，2n-1}，分組密碼是由密鑰k=(k0，k1，k2，…，kt-1)確定的一個一一映射，也就是空間{0，1，…，2n-1}，到自身的一個置換F，由於置換F是由密鑰k所確定，一般地，我們把這個置換表示為C=Fk(m)。
算法要求
分組長度足夠大
當分組長度較小時，分組密碼類似於古典的代替密碼，它仍然保留了明文的統計信息，這種統計信息將給攻擊者留下可乘之機，攻擊者可以有效地窮舉明文空間，得到密碼變換本身。
密鑰量足夠大
分組密碼的密鑰所確定密碼變換隻是所有置換中極小一部分。如果這一部分足夠小，攻擊者可以有效地窮舉明文空間所確定所有的置換。這時，攻擊者就可以對密文進行解密，以得到有意義的明文。
密碼變換足夠複雜
使攻擊者除了窮舉法以外，找不到其他快捷的破譯方法。
技術總結
優點
明文信息良好的擴展性，對插入的敏感性，不需要密鑰同步，較強的適用性，適合作為加密標準。
缺點
加密速度慢，錯誤擴散和傳播。
分組密碼將定長的明文塊轉換成等長的密文，這一過程在秘鑰的控制之下。使用逆向變換和同一密鑰來實現解密。對於當前的許多分組密碼，分組大小是 64 位，但這很可能會增加。
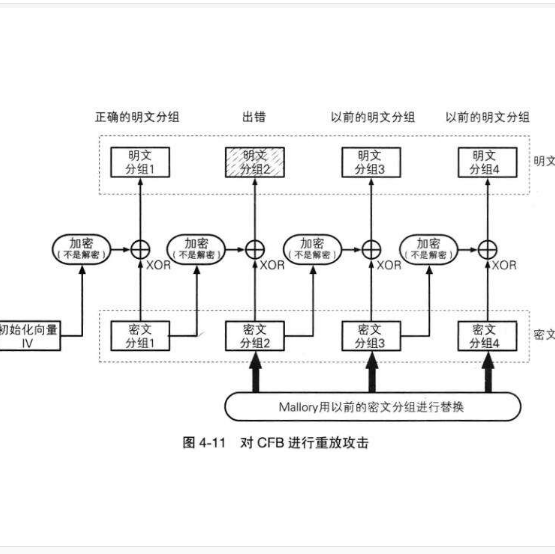
明文訊息通常要比特定的分組大小長得多，而且使用不同的技術或操作方式。這樣的方式示例有：電子編碼本（ECB）、密碼分組連結（CBC）或密碼反饋（CFB）。ECB 使用同一個密鑰簡單地將每個明文塊一個接一個地進行加密；在 CBC 方式中，每個明文塊在加密前先與前一密文塊進行“異或”運算，從而增加了複雜程度，可以使某些攻擊更難以實施。 “輸出反饋”方式（OFB）類似 CBC 方式，但是進行“異或”的量是獨立生成的。 CBC 受到廣泛使用，例如在 DES（qv）實現中，而且在有關密碼術的技術性方面的相應書籍中深入討論了各種方式。請注意：您自己建立的 密碼系統的普遍弱點就是以簡單的形式來使用某些公開的算法，而不是以提供了額外保護的特定方式使用。
