基本介紹
介紹,歷史,理論工作,構造細節,非平衡Feistel密碼,其他用途,Feistel網路作為設計組件,Feistel密碼列表,
介紹
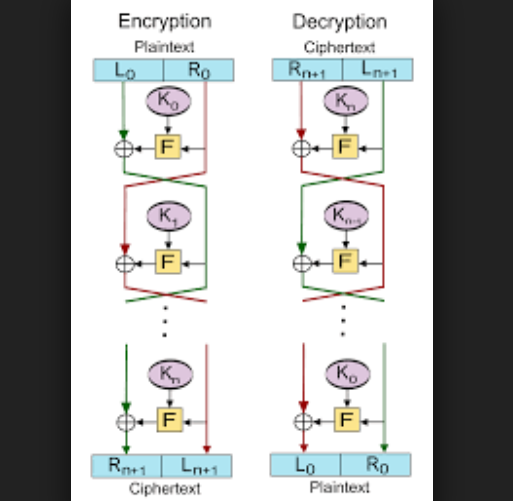
在密碼學中,費斯妥密碼(英語:Feistel cipher)是用於構造分組密碼的對稱結構,以德國出生的物理學家和密碼學家霍斯特·費斯妥(Horst Feistel)命名,他在美國IBM工作期間完成了此項開拓性研究。通常也稱為費斯妥網路(Feistel network)。大部分分組密碼使用該方案,包括數據加密標準(DES)。費斯妥結構的優點在於加密和解密操作非常相似,在某些情況下甚至是相同的,只需要逆轉密鑰編排。因此,實現這種密碼所需的代碼或電路大小能幾乎減半。
費斯妥網路是一種疊代密碼,其中的內部函式稱為輪函式。
歷史
Feistel網路最初在IBM的Lucifer密碼中商業化,這種密碼由霍斯特·費斯妥和Don Coppersmith於1973年設計。美國聯邦政府在設計DES(基於Lucifer密碼,由NSA進行修改)時採用了Feistel網路。像DES的其他組件一樣,Feistel構造中的疊代特性使得在硬體中(特別是在設計DES時已有的硬體上)實現密碼系統更容易。
理論工作
許多現代及一些較舊的對稱分組密碼基於Feistel網路(例如GOST 28147-89分組密碼),且密碼學家已經深入研究了Feistel密碼的結構和性質。具體而言,Michael Luby和Charles Rackoff分析了Feistel密碼的構造,證明了如果輪函式是一個密碼安全的偽隨機函式,使用Ki作為種子,那么3輪足以使這種分組密碼成為偽隨機置換,而4輪可使它成為“強”偽隨機置換(這意味著,對可以得到其逆排列諭示的攻擊者,它仍然是偽隨機的)。
由於Luby和Rackoff的結果非常重要,Feistel密碼有時也稱為Luby-Rackoff分組密碼。進一步的理論工作對其進行了推廣,給出了更加精確的安全界限。
構造細節
令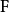 為輪函式,並令
為輪函式,並令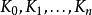 分別為輪
分別為輪 的子密鑰。
的子密鑰。
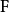
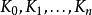

基本操作如下:
將明文塊拆分為兩個等長的塊,( )
)

對每輪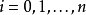 ,計算
,計算
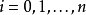
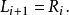

則密文為 。
。

解密密文 則通過計算
則通過計算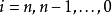

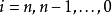

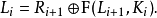
則 就是明文。
就是明文。

與代換-置換網路相比,Feistel模型的一個優點是輪函式 不必是可逆的。
不必是可逆的。

非平衡Feistel密碼
非平衡Feistel密碼相比其有所修改,其中L0和R0的長度不等。Skipjack密碼就是這種密碼的一個例子。德州儀器數字簽名轉發器使用專有的非平衡Feistel密碼來執行挑戰-回響認證。
Thorp shuffle是一種非平衡Feistel密碼的極端情況,其中一邊只有一位。這比平衡Feistel密碼具有更好的可證明安全性,但需要更多輪。
其他用途
除了分組密碼外,Feistel結構也用於其他密碼算法。例如,最優非對稱加密填充(OAEP)在某些非對稱密鑰加密方案中,使用簡單的Feistel網路對密文進行隨機化。