基本介紹
加密技術,密碼學,相關概念,對稱密碼算法,公開密碼算法,單向散列函式,數字簽名,加密算法,
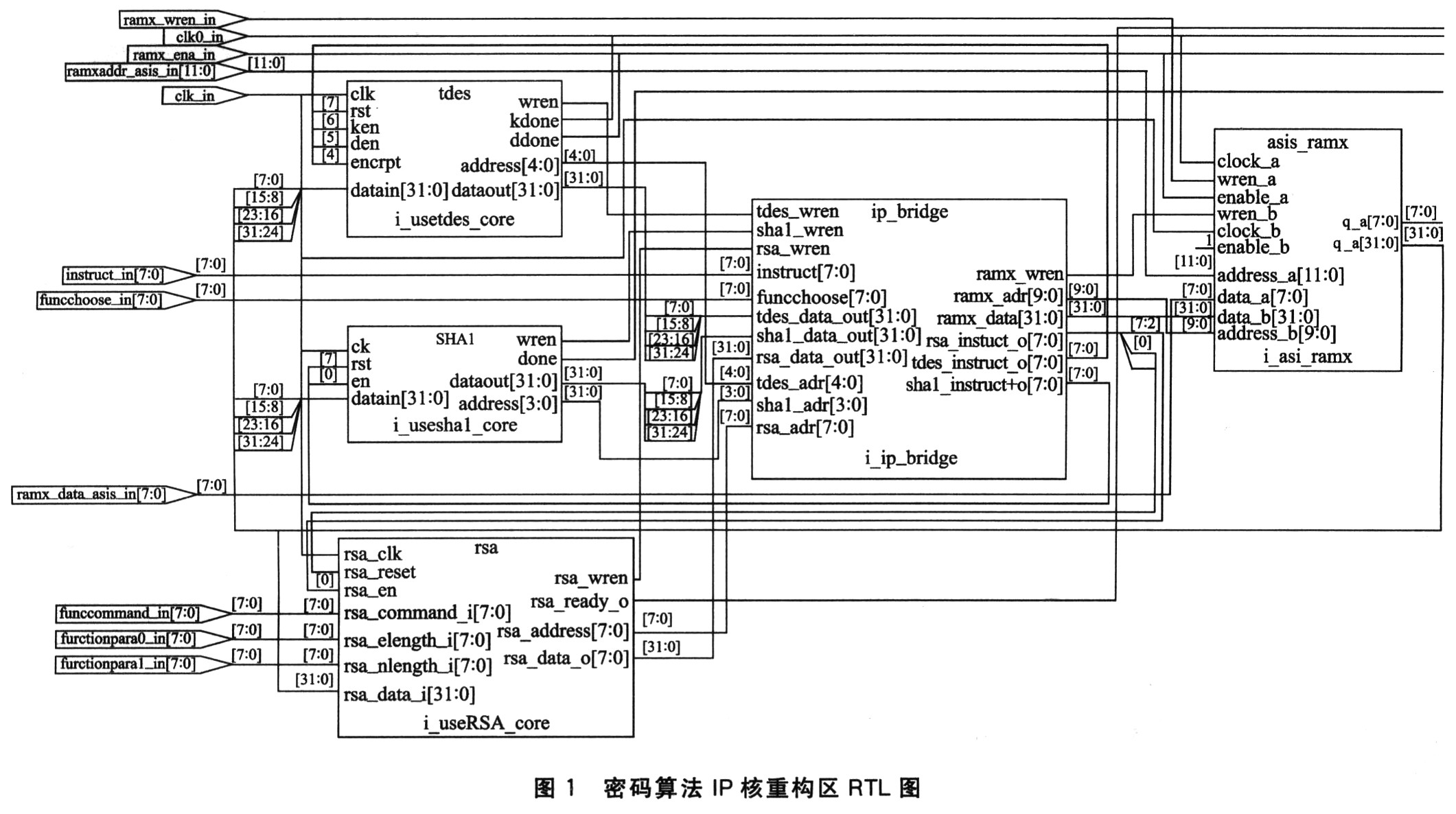
加密技術
一個密碼系統的安全性只在於密鑰的保密性，而不在算法的保密性。 對純數據的加密的確是這樣。對於你不願意讓他看到這些數據（數據的明文）的人，用可靠的加密算法，只要破解者不知道被加密數據的密碼，他就不可解讀這些數據。 但是，軟體的加密不同於數據的加密，它只能是“隱藏”。不管你願意不願意讓他（合法用戶，或 Cracker）看見這些數據（軟體的明文），軟體最終總要在機器上運行，對機器，它就必須是明文。既然機器可以“看見”這些明文，那么 Cracker，通過一些技術，也可以看到這些明文。 於是，從理論上，任何軟體加密技術都可以破解。只是破解的難度不同而已。有的要讓最高明的 Cracker 忙上幾個月，有的可能不費吹灰之力，就被破解了。
密碼學
相關概念
(1) 傳送者和接收者
假設傳送者想傳送訊息給接收者，且想安全地傳送信息：她想確信偷聽者不能閱讀傳送的訊息。
(2) 訊息和加密
訊息被稱為明文。用某種方法偽裝訊息以隱藏它的內容的過程稱為加密，加了密的訊息稱為密文，而把密文轉變為明文的過程稱為解密。
明文用M（訊息）或P（明文）表示，它可能是比特流（文本檔案、點陣圖、數位化的語音流或數位化的視頻圖像）。至於涉及到計算機，P是簡單的二進制數據。明文可被傳送或存儲，無論在哪種情況，M指待加密的訊息。
密文用C表示，它也是二進制數據，有時和M一樣大，有時稍大（通過壓縮和加密的結合，C有可能比P小些。然而，單單加密通常達不到這一點）。加密函式E作用於M得到密文C，用數學表示為：
E（M）=C.
相反地，解密函式D作用於C產生M
D（C）=M.
先加密後再解密訊息，原始的明文將恢復出來，下面的等式必須成立：
D（E（M））=M
(3) 鑑別、完整性和抗抵賴
除了提供機密性外，密碼學通常有其它的作用：.
(a) 鑑別
訊息的接收者應該能夠確認訊息的來源；入侵者不可能偽裝成他人。
(b) 完整性檢驗
訊息的接收者應該能夠驗證在傳送過程中訊息沒有被修改；入侵者不可能用假訊息代替合法訊息。
(c) 抗抵賴
傳送者事後不可能虛假地否認他傳送的訊息。
(4) 算法和密鑰
密碼算法也叫密碼，是用於加密和解密的數學函式。（通常情況下，有兩個相關的函式：一個用作加密，另一個用作解密）
如果算法的保密性是基於保持算法的秘密，這種算法稱為受限制的算法。受限制的算法具有歷史意義，但按現在的標準，它們的保密性已遠遠不夠。大的或經常變換的用戶組織不能使用它們，因為每有一個用戶離開這個組織，其它的用戶就必須改換另外不同的算法。如果有人無意暴露了這個秘密，所有人都必須改變他們的算法。
但是，受限制的密碼算法不可能進行質量控制或標準化。每個用戶組織必須有他們自己的唯一算法。這樣的組織不可能採用流行的硬體或軟體產品。但竊聽者卻可以買到這些流行產品並學習算法，於是用戶不得不自己編寫算法並予以實現，如果這個組織中沒有好的密碼學家，那么他們就無法知道他們是否擁有安全的算法。
儘管有這些主要缺陷，受限制的算法對低密級的套用來說還是很流行的，用戶或者沒有認識到或者不在乎他們系統中內在的問題。
現代密碼學用密鑰解決了這個問題，密鑰用K表示。K可以是很多數值里的任意值。密鑰K的可能值的範圍叫做密鑰空間。加密和解密運算都使用這個密鑰（即運算都依賴於密鑰，並用K作為下標表示），這樣，加/解密函式現在變成：
EK(M)=C
DK(C)=M.
這些函式具有下面的特性：
DK（EK（M））=M.
有些算法使用不同的加密密鑰和解密密鑰，也就是說加密密鑰K1與相應的解密密鑰K2不同，在這種情況下：
EK1(M)=C
DK2(C)=M
DK2 (EK1(M))=M
所有這些算法的安全性都基於密鑰的安全性；而不是基於算法的細節的安全性。這就意味著算法可以公開，也可以被分析，可以大量生產使用算法的產品，即使偷聽者知道你的算法也沒有關係；如果他不知道你使用的具體密鑰，他就不可能閱讀你的訊息。
密碼系統由算法、以及所有可能的明文、密文和密鑰組成的。
對稱密碼算法
對稱算法有時又叫傳統密碼算法，就是加密密鑰能夠從解密密鑰中推算出來，反過來也成立。在大多數對稱算法中，加/解密密鑰是相同的。這些算法也叫秘密密鑰算法或單密鑰算法，它要求傳送者和接收者在安全通信之前，商定一個密鑰。對稱算法的安全性依賴於密鑰，泄漏密鑰就意味著任何人都能對訊息進行加/解密。只要通信需要保密，密鑰就必須保密。
對稱算法的加密和解密表示為：
EK（M）=C
DK（C）=M
對稱算法可分為兩類。一次只對明文中的單個比特（有時對位元組）運算的算法稱為序列算法或序列密碼。另一類算法是對明文的一組比特亞行運算，這些比特組稱為分組，相應的算法稱為分組算法或分組密碼。現代計算機密碼算法的典型分組長度為64比特——這個長度大到足以防止分析破譯，但又小到足以方便使用（在計算機出現前，算法普遍地每次只對明文的一個字元運算，可認為是序列密碼對字元序列的運算）。
公開密碼算法
公開密鑰算法（也叫非對稱算法）是這樣設計的：用作加密的密鑰不同於用作解密的密鑰，而且解密密鑰不能根據加密密鑰計算出來（至少在合理假定的長時間內）。之所以叫做公開密鑰算法，是因為加密密鑰能夠公開，即陌生者能用加密密鑰加密信息，但只有用相應的解密密鑰才能解密信息。在這些系統中，加密密鑰叫做公開密鑰（簡稱公鑰），解密密鑰叫做私人密鑰（簡稱私鑰）。私人密鑰有時也叫秘密密鑰。為了避免與對稱算法混淆，此處不用秘密密鑰這個名字。
用公開密鑰K加密表示為
EK(M)=C.
雖然公開密鑰和私人密鑰是不同的，但用相應的私人密鑰解密可表示為：
DK(C)=M
有時訊息用私人密鑰加密而用公開密鑰解密，這用於數字簽名（後面將詳細介紹），儘管可能產生混淆，但這些運算可分別表示為：
EK(M)=C
DK(C)=M
當前的公開密碼算法的速度，比起對稱密碼算法，要慢的多，這使得公開密碼算法在大數據量的加密中套用有限。
單向散列函式
單向散列函式 H(M) 作用於一個任意長度的訊息 M，它返回一個固定長度的散列值 h，其中 h 的長度為 m 。
輸入為任意長度且輸出為固定長度的函式有很多種，但單向散列函式還有使其單向的其它特性：
(1) 給定 M ，很容易計算 h ；
(2) 給定 h ，根據 H(M) = h 計算 M 很難 ；
(3) 給定 M ，要找到另一個訊息 M‘ 並滿足 H(M) = H(M’) 很難。
在許多套用中，僅有單向性是不夠的，還需要稱之為“抗碰撞”的條件：
要找出兩個隨機的訊息 M 和 M‘，使 H(M) = H(M’) 滿足很難。
由於散列函式的這些特性，由於公開密碼算法的計算速度往往很慢，所以，在一些密碼協定中，它可以作為一個訊息 M 的摘要，代替原始訊息 M，讓傳送者為 H(M) 簽名而不是對 M 簽名 。
如 SHA 散列算法用於數字簽名協定 DSA中。
數字簽名
提到數字簽名就離不開公開密碼系統和散列技術。
有幾種公鑰算法能用作數字簽名。在一些算法中，例如RSA，公鑰或者私鑰都可用作加密。用你的私鑰加密檔案，你就擁有安全的數字簽名。在其它情況下，如DSA，算法便區分開來了??數字簽名算法不能用於加密。這種思想首先由Diffie和Hellman提出 。
基本協定是簡單的 ：
(2) A 將簽名的檔案傳給B。
(3) B用A的公鑰解密檔案，從而驗證簽名。
這個協定中，只需要證明A的公鑰的確是她的。如果B不能完成第（3）步，那么他知道簽名是無效的。
這個協定也滿足以下特徵：
(1) 簽名是可信的。當B用A的公鑰驗證信息時，他知道是由A簽名的。
(2) 簽名是不可偽造的。只有A知道她的私鑰。
(3) 簽名是不可重用的。簽名是檔案的函式，並且不可能轉換成另外的檔案。
(4) 被簽名的檔案是不可改變的。如果檔案有任何改變，檔案就不可能用A的公鑰驗證。
(5) 簽名是不可抵賴的。B不用A的幫助就能驗證A的簽名。
加密算法
加密技術是對信息進行編碼和解碼的技術，編碼是把原來可讀信息（又稱明文）譯成代碼形式（又稱密文），其逆過程就是解碼（解密）。加密技術的要點是加密算法，加密算法可以分為對稱加密、不對稱加密和不可逆加密三類算法。
對稱加密算法 對稱加密算法是套用較早的加密算法，技術成熟。在對稱加密算法中，數據發信方將明文（原始數據）和加密密鑰一起經過特殊加密算法處理後，使其變成複雜的加密密文傳送出去。收信方收到密文後，若想解讀原文，則需要使用加密用過的密鑰及相同算法的逆算法對密文進行解密，才能使其恢復成可讀明文。在對稱加密算法中，使用的密鑰只有一個，發收信雙方都使用這個密鑰對數據進行加密和解密，這就要求解密方事先必須知道加密密鑰。對稱加密算法的特點是算法公開、計算量小、加密速度快、加密效率高。不足之處是，交易雙方都使用同樣鑰匙，安全性得不到保證。此外，每對用戶每次使用對稱加密算法時，都需要使用其他人不知道的惟一鑰匙，這會使得發收信雙方所擁有的鑰匙數量成幾何級數增長，密鑰管理成為用戶的負擔。對稱加密算法在分散式網路系統上使用較為困難，主要是因為密鑰管理困難，使用成本較高。在計算機專網系統中廣泛使用的對稱加密算法有DES和IDEA等。美國國家標準局倡導的AES即將作為新標準取代DES。
不對稱加密算法 不對稱加密算法使用兩把完全不同但又是完全匹配的一對鑰匙—公鑰和私鑰。在使用不對稱加密算法加密檔案時，只有使用匹配的一對公鑰和私鑰，才能完成對明文的加密和解密過程。加密明文時採用公鑰加密，解密密文時使用私鑰才能完成，而且發信方（加密者）知道收信方的公鑰，只有收信方（解密者）才是唯一知道自己私鑰的人。不對稱加密算法的基本原理是，如果發信方想傳送只有收信方才能解讀的加密信息，發信方必須首先知道收信方的公鑰，然後利用收信方的公鑰來加密原文；收信方收到加密密文後，使用自己的私鑰才能解密密文。顯然，採用不對稱加密算法，收發信雙方在通信之前，收信方必須將自己早已隨機生成的公鑰送給發信方，而自己保留私鑰。由於不對稱算法擁有兩個密鑰，因而特別適用於分散式系統中的數據加密。廣泛套用的不對稱加密算法有RSA算法和美國國家標準局提出的DSA。以不對稱加密算法為基礎的加密技術套用非常廣泛。
不可逆加密算法 的特徵是加密過程中不需要使用密鑰，輸入明文後由系統直接經過加密算法處理成密文，這種加密後的數據是無法被解密的，只有重新輸入明文，並再次經過同樣不可逆的加密算法處理，得到相同的加密密文並被系統重新識別後，才能真正解密。顯然，在這類加密過程中，加密是自己，解密還得是自己，而所謂解密，實際上就是重新加一次密，所套用的“密碼”也就是輸入的明文。不可逆加密算法不存在密鑰保管和分發問題，非常適合在分散式網路系統上使用，但因加密計算複雜，工作量相當繁重，通常只在數據量有限的情形下使用，如廣泛套用在計算機系統中的口令加密，利用的就是不可逆加密算法。近年來，隨著計算機系統性能的不斷提高，不可逆加密的套用領域正在逐漸增大。在計算機網路中套用較多不可逆加密算法的有RSA公司發明的MD5算法和由美國國家標準局建議的不可逆加密標準SHS(Secure Hash Standard:安全雜亂信息標準)等。
