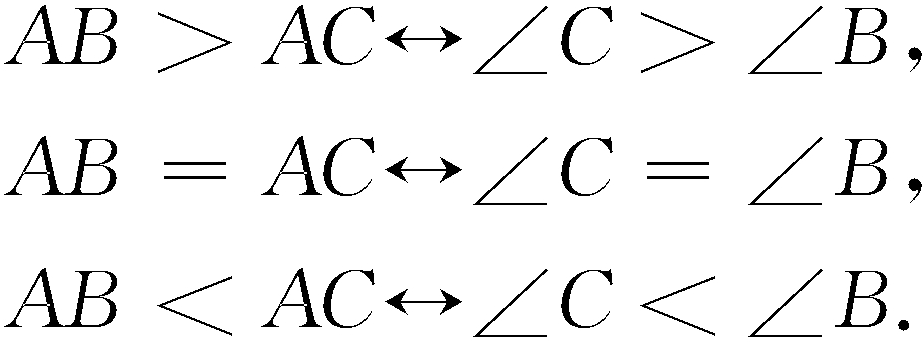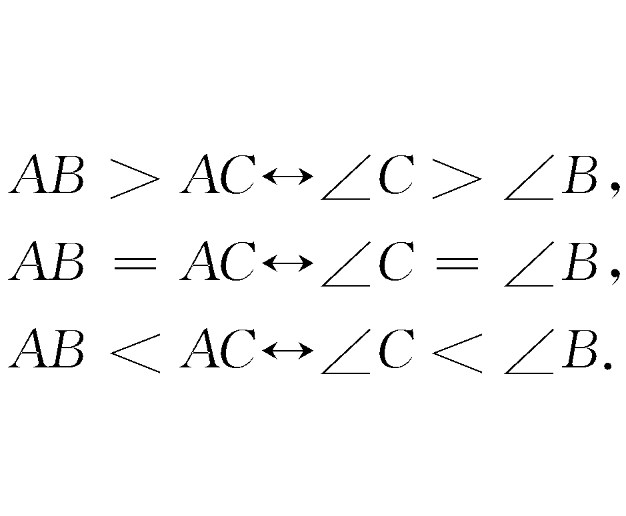分斷式命題(respectively assertive proposition)是一種複合命題，若一個命題是由A1→B1，A2→B2，…，An→Bn這兒個命題組成，A1，A2，…，An和B1，B2，…，Bn分別包含了條件和結論的所有可能，並且A1，A2，…，An互不相容，B1，B2，…Bn也互不相容，則稱這樣的命題為分斷式命題。例如，在平面內有一直線l與半徑為r的圓，設圓心到直線l的距離為d，當d>r時，直線l與圓相離，當d=r時，直線l與圓相切，當d<r時，直線l與圓相交，這個命題就是一個分斷式命題。在邏輯學中，若一組命題滿足上述條件，則稱這一組命題構成一個閉系統，因此，若一個分斷式命題為真，那么它的逆命題一定為真。
基本介紹
- 中文名：分斷式命題
- 外文名：respectively assertive proposition
- 所屬學科：數學（邏輯學）
- 簡介：一種複合命題
基本介紹,舉例說明,
基本介紹
分斷式命題是一種複合命題，判定某類數學命題真假時使用的一種命題形式，由若干個命題組合而成的那個命題，其中這若干個命題的條件和結論一一對應互不相容、窮盡各種可能。如果一個分斷式命題是正確的，則它的逆命題也是正確的。如果一個命題具有下述形式：
並且A1∨A2∨…∨An和B1∨B2∨…∨Bn均為真命題，Ai∧Aj和Bi∧Bj(i≠j，i，j=1，2，…，n)恆為假命題，則這個命題稱為分斷式命題，亦稱這個命題構成一個閉系統。
分斷式命題或者是將原命題與逆命題合併敘述，或者是把其中各個命題(或一部分命題)拆開來分條敘述。
舉例說明
【例1】在實係數方程ax2+bx+c=0(a≠0)的理論中，命題：
1.如果Δ=b2-4ac>0，則它有兩個不相等的實根；
2.如果Δ=b2-4ac=0，則它有兩個相等的實根；
3.如果Δ=b2-4ac<0，則它無實根。
該命題就是一個分斷式命題。
【例2】在△ABC中：
1.AB>AC
∠C>∠B;
2.AB=AC∠C=∠B;
3.AB<AC∠C<∠B
組合而成的一個命題就是一個分斷式命題。
其中包含了兩線段AB，AC之間所有可能的三種關係和兩角∠B，∠C之間相應的三種關係，條件與結論一一對應
正確的分斷式命題稱為配套定理。
【例3】定理“在同圓或等圓中，等弦距圓心等遠，不等弦距圓心不等遠，大者距離較近，小者距離較遠”，其中前提把兩弦的大小關係“等於”、 “大於”、“小於” 一一道盡；而結論把兩弦與圓心的遠近關係“等遠”、“較近” 、“較遠” 一一說完。而且這些關係又都是互不相容的，所以這個定理是分斷式命題。
