分散控制問題解法

求解分散控制問題的計算方法。分散控制採用非經典信息結構，為了求得問題的解，一般要作某些假設。不同的假設條件可得到多種不同的簡化模型。對某一簡化模型也有多種不同的解法。

基本介紹

• 中文名：分散控制問題解法
• 詳細內容：按信息結構和控制器結構
• 理論發展：控制共享模式
• 站間：站間有部分信息交換

詳細內容

按信息結構和控制器結構，分散控制問題解法有以下三類。

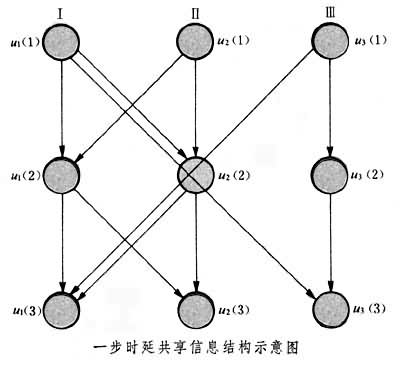
一步時延共享信息結構

非經典信息結構會導致控制器無限維，控制律為非線性，而難以求得顯式解。但也存在一類特殊問題，即一步時延共享信息結構的離散系統問題,它能滿足分離原理,能將估計問題與控制問題分開，得到線性最優解。所謂一步時延共享信息結構是指每個控制站在時刻 k能獲得從時刻0到時刻k-1包括本站在內的整體系統的全部輸入和輸出信息，而在時刻 k只能獲得本站的觀測信息。此處，輸入指施加於受控對象上的控制，輸出指從控制站對受控對象的觀測。在這種情況下，各站的控制只依賴各站本身占有的信息，包括 k-1時刻以前本站和其他各站經通信道送來的全部歷史信息以及 k時刻本站即時觀測信息。下圖為兩控制站間的信息交換情況。每一節點對應於某一離散時刻 k，從一點到另一點為一步。在k=2時，Ⅰ站接收k=1步時的u1(1)和u2(1)，Ⅱ站接收u2(1)和u1(1)，即u1(1)和u2(1)是Ⅰ、Ⅱ站共享的信息。若另有Ⅲ站通過Ⅱ而與Ⅰ耦合，則Ⅰ、Ⅲ便破壞了一步時延關係而變成了二步時延。這樣的信息結構可歸入隊決策理論中部分嵌套信息結構類中。它可以簡化為等效的靜態隊決策問題，從而可用部分嵌套法求解。也可用離散最小值原理求解，但運算較複雜。較方便的是用動態規劃法把整個 N步的動態問題分解為 N個靜態隊決策問題求解。以上各法線上性二次型高斯(LQG)問題的情況下,最優控制律均可表達成觀測數據的線性函式。

固定控制器結構且站間無信息交換

為了避開二次推測現象(見大系統分散控制理論)，假定控制器的結構為有限維且等於受控對象的維數。限定控制律是本站累積的測量信息的線性函式。站間無線上信息交換，只利用本站的觀測來對系統進行狀態估計。這時分離定理不成立。考慮到各站是合作關係，最最佳化的計算宜以組合的方式進行，即同時求取所有各站的“最優”的線性控制律和濾波器參數。由此導出的一種直接算法是按無偏估計的原則把各控制站方程與受控對象方程組合成集中方程的形式，並對隨機量取其協方差矩陣，從而將一個隨機型分散問題轉換成等價的確定型集中問題，這種問題可用矩陣最小值原理法求解，但必須求解難度大的矩陣兩點邊界值問題。此法還存在維數擴展現象，即集中方程的維數等於受控對象維數的(N+1)倍。N為控制站數。

固定控制器結構但站間有部分信息交換

假定控制器維數等於受控對象的維數，控制律為線性律。一種典型模式是站間只交換各局部濾波器對系統的狀態估計值而不交換控制量信息。這時分離定理不成立。最最佳化計算仍可按組合方式進行。通常只考慮最最佳化時間為無限長的情況。直接把控制器方程與受控對象方程組合成集中方程，把問題轉換為等價的確定型參數最最佳化問題。這樣就可以用多種數學規劃方法求解。但一般要解李雅普諾夫方程，因有一定限制不能保證最優解一定存在。維數擴展現象仍不可避免。

理論發展

除上面三種典型簡化模式的解法外，還有所謂控制共享模式，即各站占有不同的整體系統初態和噪聲的先驗知識，站間只交換控制量而不交換狀態估計值。還有一種所謂遞階模式，即站間不直接交換信息但通過上級協調器交換信息。協調器具有整體先驗知識，知道下級子系統的動態特性和它們的關聯情況。下級控制器只知道根據本身的動態特性，觀測值和控制量。上級周期性地對下級進行協調，實際上就是交換信息。這兩種簡化模式都具有相應的解法。