分布參數電路

分布參數電路是指在高頻工作下,傳輸線的分布參數效應不能被忽略，其電氣特性由單位線長上的分布電感、分布電容、分布電阻和分布電導來描述，這時傳輸線已與串聯電感和電阻、並聯電容和電導融為一體，利用傳輸線的分布參數特性所組成的電路就稱為分布參數電路，以這區別於由集總參數元件組成的集總參數電路。

基本介紹

• 中文名：分布參數電路
• 外文名：Distributed Parameter Circuit
• 簡介：一個電路應該作為集總參數電路
• 簡史：19世紀中葉
• 分析方法：對分布參數電路進行分析時

基本信息

一個電路應該作為集總參數電路，還是作為分布參數電路，或者說，要不要考慮參數的分布性，取決於其本身的線性尺寸與表征其內部電磁過程的電壓、電流的波長之間的關係。若用 l表示電路本身的最大線性尺寸，用λ表示電壓或電流的波長，若滿足l<0.1*λ，電路便可視為集總參數電路，否則便需作為分布參數電路處理。

在電力系統中，高電壓遠距離的電力傳輸線是比較典型的分布參數電路。因為這種電路雖然電壓、電流的頻率很低(50Hz)，波長很長（6000公里），但其長度卻達數百公里甚至幾千公里,已可與波長相比擬。另外,在通信系統中所用的信號傳輸線、發射天線和接收天線等的實際尺寸並不太長，但傳送的信號卻頻率高、波長短，所以也應作為分布參數電路處理。

研究分布參數電路時，常以具有兩條平行導線、而且參數沿線均勻分布的傳輸線為對象。這種傳輸線稱為均勻傳輸線（或均勻長線）。作這樣的選擇是因為實際套用的傳輸線可以等效轉換成具有兩條平行導線形式的傳輸線，而且這種均勻的傳輸線容易分析。

簡史

對分布參數電路的研究始於19世紀中葉。1856年物理學家開爾文針對當時利用海底電纜傳送電報出現的信號延遲、畸變和變弱的現象，首先提出了海底電纜的理論，成為研究分布參數電路的先驅。1893年，英國工程師O.亥維賽利用J.C.麥克斯韋的自由空間電磁波理論,對二線傳輸線（包括同軸傳輸線）導引的電磁波,首次提出了簡明而又普遍化的解釋，從而全面地建立了傳輸線（長線）的經典理論。

分析方法

在電路理論中，對分布參數電路進行分析時，首先是建立模型。建立模型採用的是無限逼近法。這種方法是將分析對象（例如均勻傳輸線）構想為許多個無窮小長度元dx。由於長度元dx是無窮小量，在這些長度元的範圍內參數可以集中。於是，每個長度元可以抽象成一個集總參數電路。而這些集總參數電路級聯而成的鏈形電路就成為整個均勻傳輸線的電路模型。顯然，只有無窮小長度元dx的個數為無限多時，鏈形電路才能準確地代表均勻傳輸線。接著是根據模型寫方程。方程是參照長度元dx抽象成的集總參數電路，利用KCL和KVL(見基爾霍夫定律)寫出的。它是一個偏微分方程組。最後是解方程求解答，再根據解答討論電路（即傳輸線）的性能。 　如果建模完成後，再用合適的實際電阻器、電感器和電容器來實現，便可得到一個線性尺寸很小的稱為人工線的實際鏈形電路。這就提供了對傳輸線進行實驗研究的條件。人們可以在實驗室內利用很短的人工線實現對長達幾百公里，甚而上千公里的輸電線上的各種工作狀態的觀察和各種數據的測量。 　分布參數電路作為一個電磁系統當然還可採用電磁場理論進行分析。這樣做雖然嚴格與精確，但並不方便，因為求解電磁場方程組要比求解電路方程組困難得多。因此，通常是採用電路理論來分析分布參數電路。 　傳輸線 　傳送能量或信號的各種傳輸線的總稱。其中包括電力傳輸線、電信傳輸線、天線等。傳輸線又稱長線。由於它具有在空間某個方向上其長度已可與其內部電壓、電流的波長相比擬，而必須考慮參數分布性的特徵，所以是典型的分布參數電路。在電路理論中討論傳輸線時以均勻傳輸線作為對象。均勻傳輸線是指參數沿線均勻分布的二線傳輸線,其基本參數,或稱原參數是R₀、L0、C₀和G₀。其中R₀ 代表單位長度線（包括來線與回線）的電阻；L₀代表單位長度來線與回線形成的電感；C₀和G0分別代表單位長度來線與回線間的電容和漏電導。這些參數是由導線所用的材料、截面的幾何形狀與尺寸、導線間的距離，以及導線周圍介質決定的。在高頻和低頻高電壓下它們都有近似的計算公式。

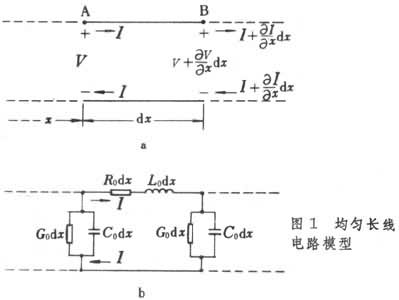
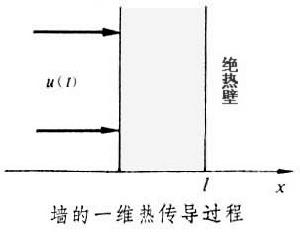
傳輸線的方程

將均勻長線分成許多長度元dχ，其中之一見圖1a。對該長度元忽略參數的分布性，可得出其集總參數電路模型（圖1b）。將每個長度元都這樣處理後，得出的由許多集總參數電路作為環節級聯而成的鏈形電路就是整個均勻長線的電路模型。若設圖1a所示長度元的A點和B點距長線的始端的距離分別為χ和χ+dχ；在某一瞬間A點的電壓為V，電流為I；在B點的電壓為V+dV,電流為I+dI， 則對此長度元的集總參數電路模型（圖1b）可用KVL和KCL導出偏微分方程組通常稱為亥維賽電報方程。在正弦穩態下，使用電壓和電流的相量可將上述方程組化為

公式

公式

式中Z0稱為線阻抗，Y0稱為線導納。 　聯立式(5)和式(6)求解，可得電壓和電流的正弦穩態解

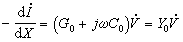公式

公式

式中A1和A2是需要根據邊界條件定出的兩個常數，通常都是複數,可分別記為A1=a1e拸$和A2=a2e拹$

公式

公式

行波、入射波和反射波 　長線的一個明顯的特徵是其電壓和電流正弦穩態解中的兩個分量的波形皆隨時間的變化而沿線移動。這種沿線向一個方向移動的波稱為行波。將式(7)和式(8)改寫成瞬時值形式

便容易證實這一點。電壓表達式右端第一項代表的電壓分量VI(χ ,t) 是以速度（稱為相速或波速）

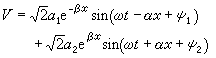公式

沿線向χ 增加方向傳播的行波，而且隨著波的前進，振幅按因子 e-βχ決定的指數律衰減。這個從始端向終端傳播的行波稱為電壓入射波。圖2a表示出 t=t0和t=t0+Δt時的VI（χ ,t）曲線。同樣，電流分量IφI(χ ,t)也是一個行波，稱為電流入射波。電壓(電流)的另一個分量VR(χ,t)·【IR(χ,t)】也是一個行波，波速也是vp。但由於相位中與χ 有關的項是αχ,而不是-αχ,所以這個波的傳播方向與VφI(χ ,t)【IφI(χ ,t)】的傳播方向相反。另外,由於因子eβχ隨χ的減少而減少，其振幅也隨著波的前進而逐漸衰減。這個從終端向始端傳播的行波稱為電壓(電流)反射波。圖2b表示的是電壓反射波VR(χ ,t)的波過程。 　式(9)和式(10)的 β和α分別稱為衰減係數和相位係數。前者決定波振幅衰減的快慢，後者決定波相位變化的快慢。

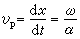公式

公式

運行狀態

用長線終端處的電壓2和電流2作為邊界條件定出常數A1和A2後,可得出用妭2和夒2表示的線上任一點處電壓和電流，即式中χ┡是從終端算起的距離。 　在長線終端處電壓和電流反射波相量分別與電壓和電流入射波相量之比稱為電壓反射係數和電流反射係數，式中ZL=妭2/夒2是負載阻抗。 　當終端所接負載阻抗ZL等於特性阻抗時，反射係數等於零,說明在這種情形下不存在反射波。均勻傳輸線不存在反射波的運行狀態稱匹配狀態,簡稱匹配。這時的負載稱為匹配負載。 因為無反射波將能量攜帶回始端(電源端)的現象發生,所以由始端送達終端（負載端）的能量將全部被負載吸收。在這種狀態下，負載吸收的功率為

公式

式中ZC和θC分別是特性阻抗的模與幅角。這一功率稱為自然功率。入端阻抗

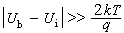公式

即從長線上任何一處向終端看去，入端阻抗均等於特性阻抗。因此，特性阻抗又稱重複阻抗。

公式

等效電路

式中夒娦前的負號表示終端電流的參考方向改選為由終端指向始端。將上述方程與二連線埠網路的含T 參數的方程比較一下發現，當只關心長線始端或終端的電壓或電流時，整個長線可視為一個無源二連線埠網路，其 T參數為線上各點的電壓和電流均隨時間t 作正弦變化， 而二者之振幅也隨χ┡作正弦變化。

公式

也就是說,在前一類點上出現電壓的波腹，在後一類點上出現電壓的波節。從電流的波形圖上看到的恰好相反,在各點上出現電流的波節，在各點上出現電流的波腹。由於這些波腹、波節都駐立不動，所以電壓、電流波亦駐立不動而成為駐波。此時入端阻抗式中X1為電抗。由此式可知入端阻抗是一純電抗，並且隨線的長度l而異，在時為容抗;在時為感抗，余類推（圖4b）。在時,入端阻抗為零,相當於電壓諧振；而在時,入端阻抗為無限大，相當電流諧振(圖4c)。 　無損耗傳輸線短路時的情況可作類似的討論，得到的結論與空載時的結論互為對偶。入端阻抗的上述性質使得無損耗傳輸線在高頻電路中獲得多方面的套用。例如開路線和短路線都可用作電抗元件，開路線可充當電容器,而的短路線則能充當電感器；又例如可利用長度等於的開路線或短路線作為具有高品質因數的振盪迴路。另外，將長為無損耗線接在一般長線與純電阻負載之間會起一個阻抗變換器的作用，使負載與長線相匹配，等等。

公式

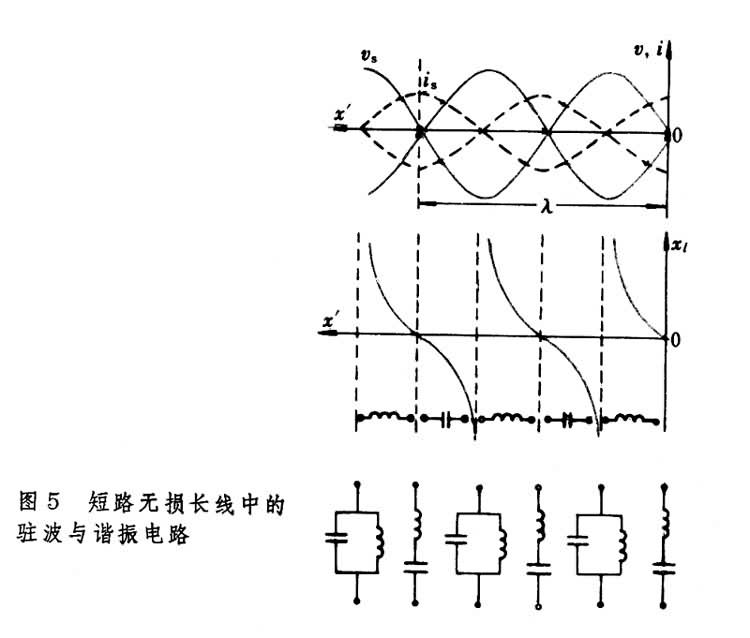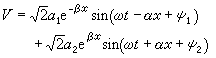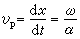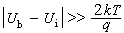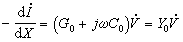公式