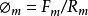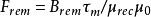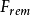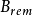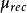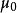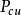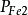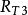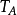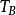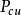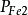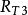集總參數電路:基本概念,電路理論的發展歷史,1) 從醞育期到獨立學科的形成,2)

集總參數思想是電路理論的最基本也是最核心的思想。

集總參數電路是由電路電氣器件的尺寸和工作信號的波長來做標準劃分的，要知道集總參數電路首先要了解實際電路的基本定義。實際電路有可分為分布參數電路和集總參數電路。

基本介紹

中文名：集總參數電路
外文名：Lumped Parameter Electrical Circuit
滿足條件：d<<λ
所屬領域：物理學，電力學
類別：電路

基本概念,電路理論的發展歷史,1) 從醞育期到獨立學科的形成,2) 經典電路理論的形成,3) 現代電路理論的開創與發展,電磁熱路中的集總參數,熱路、磁路和熱路簡單建模,集總參數電路模型,集總參數磁路模型,集總參數熱路模型,

基本概念

由電阻器、電容器、線圈、變壓器、電晶體、運算放大器、傳輸線、電池、發電機和信號發生器等電氣器件和設備連線而成的電路，稱為實際電路。以電路電氣器件的實際尺寸(d)和工作信號的波長(λ)為標準劃分，實際電路又可分為集總參數電路和分布參數電路。

滿足d<<λ條件的電路稱為集總參數電路。其特點是電路中任意兩個端點間的電壓和流入任一器件端鈕的電流完全確定，與器件的幾何尺寸和空間位置無關。

不滿足d<<λ條件的電路稱為分布參數電路。其特點是電路中的電壓和電流是時間的函式而且與器件的幾何尺寸和空間位置有關。有波導和高頻傳輸線組成的電路是分布參數電路的典型例子。

電路理論的發展歷史

迄今為止，關於電路理論和電路課程的歷史，怎樣分段，並沒有一個統一的看法，不同的考察者有不同的認識我們認為，從19世紀初時伏特發明電池( 1800年) 至今可以劃分為以下三個階段：

1) 從醞育期到獨立學科的形成

19世紀20年代至20世紀40年代

19世紀20年代至20世紀初，電力工業和初期通訊服務事業的興起推動了電路理論學科的醞育和形成這一時期，發現了電流的磁效應( 1820) 和電磁感應現象( 1831) ; 發明了電動機發電機( 1866) 變壓器( 1881) 電報( 1838) 電話( 1876)電燈( 1879) 和無線電( 1894) 等; 出現了歐姆定律( 1826) 電磁感應定律( 1831) 基爾霍夫定律( 1845) 和麥克斯韋方程組( 1869) ; 證實了電磁波的存在( 1889) 在分析方法上出現了電阻電容和電感模型的初步概念( 1853) 磁路的歐姆定律(1880) 分析交流電路的複數符號法( 1893) 阻抗的概念( 1911) 和Foster電抗定理( 1924) 最初，學校中電工教育的內容被看成是物理學中電磁學的一個分支包括直流電路交流電路三相電路發電機電動機變壓器電工測量和配電系統等兩電訊內容很少，網路綜合的概念尚未建立，電路設計多憑經驗。

20世紀初至40年代，證明了電子的存在，發明了電子管( 真空三極體，1907) 放大器振盪電路( 1914) 和電視( 1925) 等為設計廣播接收和傳送等技術的需要，出現了網路綜合逼近理論( 1930)正實函式的概念( 1931) 和網路函式的概念( 1936)進入40年代之後，電路理論逐步脫離電磁學形成了一門包含有電路分析和電路綜合的獨立學科。

2) 經典電路理論的形成

20世紀40年代至20世紀50年代

第二次世界大戰期間，雷達微波脈衝技術控制系統和電子儀器等的發展構成了電路理論進一步發展的新背景約在1947年發明了電晶體。40年代末至50年代初，美國麻省理工學院Guillemin教授對電路理論進行了全面系統的總結，編著了電路理論導論一書，IntroductoryCircuitTheory ，NewYork: Wiley，1953 這是一本具有里程碑式的著作，它標誌了經典電路理論或稱傳統電路理論的形成。

所謂經典電路理論或稱傳統電路理論是指它的內容只涉及線性非時變無源和雙向的RLC元件組成的電路 Guillemin教授對電路理論總結的要點是: ①強調並落實了基本原理的重要性; ②對上述電路的分析給出了適用範圍極寬的系統的理論與方法; ③給出了更符合認識規律的先動態後穩態( 或更確切說是先時域分析後正弦穩態分析) 的敘述體系。

3) 現代電路理論的開創與發展

20世紀50年代中至今

20世紀50年代中期以後，電晶體繼續發展後，又發明了積體電路( 1958) ，電晶體計算機( 1959) 和積體電路計算機( 1964) 等 20世紀60年代末70年代初，在電路技術的理論概括方面出現了現代電路理論的內容

所謂現代電路理論是指其內容不只涉及線性非時變無源雙向和二端元件組成的電路，還涉及到非線性時變有源和多端元件組成的電路其分析工具或手段不僅依靠人工手算，還要充分利用計算機輔助分析也就是說，電路理論不但要成為對線性非時變無源雙向的電阻器電感器電容器耦合電感和理想變壓器等所謂電工元件組成的電路進行分析和綜合的基礎，還要成為包括非線性時變有源多端的電晶體和積體電路等所謂電子元件組成的電路( 包括模擬電路，也包括數字電路) 進行分析和綜合的基礎。

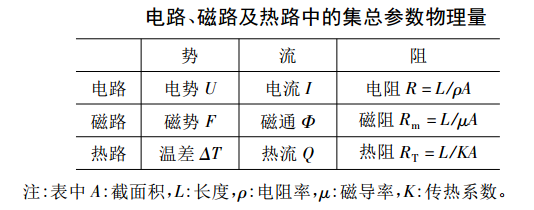
電磁熱路中的集總參數

對於基本電路模型中，流過電阻上的電流為

I=U/R （1）

式中，U為電阻兩端的電勢差，R為電阻值基本電路中的電勢電流和電阻，都是集總參數在磁路熱路的分析中，也是依據於類似的最基本的勢流和阻的概念磁路中的三個基本物理量分別為磁勢Fm 磁通

和磁阻Rm 它們之間的基本關係為

（2）

熱路中的勢流及阻所對應的物理量則分別為溫度差△T，熱流Q及熱阻R_T兩個物體或者一個物體的兩個位置處存在溫度差△T，熱量則會經由熱傳導對流換熱及熱輻射的方式由溫度高的地方流向溫度低的地方，即產生熱流Q，而熱量流動速率取決於溫度差以及熱路中的熱阻R_T，可以表示為

Q= △T/R_{T （3）}

熱路、磁路和熱路簡單建模

集總參數電路模型

對於對稱三相電機，可以選取一相進行分析，外部電源供給每相繞組上的電壓降，由電阻壓降繞組感應反電勢組成，如圖所示:

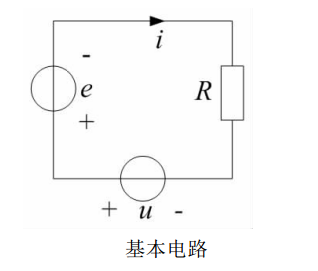
由於各物理量均為隨時間變化的量，電壓u與電機驅動控制器等有關，反電勢e與電機內磁場變化繞組匝數等密切相關由於不是本文關注內容，在此不贅述它們均以小寫字元表示在任意時刻，該相繞組中的電流均可表示為

i =( u－e) /R ( 4)

集總參數磁路模型

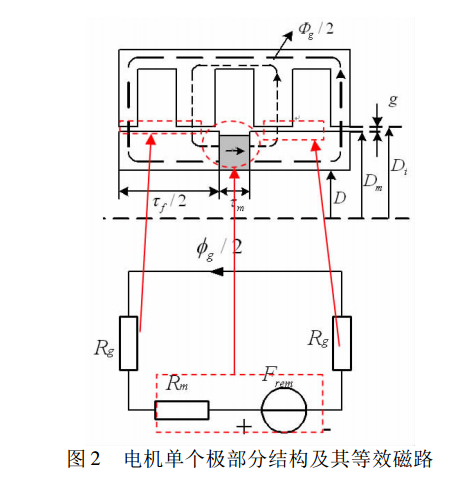
為簡化分析，選取電機單個極結構進行磁路分析圖中所示為RZ坐標系下電機的單個極結構，其所對應的等效磁路圖磁路中，由於鐵心的磁導率是空氣磁導率的幾千倍，因此忽略鐵心中飽和，認為理想情況下，鐵心的磁導率近似於無窮大因此在該磁路中，鐵心上的磁阻可以忽略永磁體為磁源，是磁路中產生磁通的來源，永磁體的磁勢為Fm，磁路中的磁壓降，主要在磁阻大的氣隙上磁勢Fm 磁通磁阻Rm的表達式分別為

(5)

式中，

為永磁體的磁勢，

為永磁體的剩餘磁感應強度，

為永磁體充磁方向厚度，

，

為磁導率永磁體的磁阻Rm及氣隙的磁阻Rg 計算，與電阻計算類似，由截面積長度磁導率決定，在此不再贅述磁通與磁勢之間的關係為

獲得了磁路中的磁通後往下分析，即可分析得到磁通密度B，輸出轉矩等參數.

集總參數熱路模型

由於具體實例的分析主要目的重在幫助學生理解集總參數概念及它們之間的關聯性，而且電路教學通常面對大二學生，考慮到他們的知識基礎，在熱路分析時，也簡化分析，僅選擇單個齒槽為分析對象，如選取圖2中單個齒槽為對象，如圖3所示，其所對應的等效熱路如圖4所示

在上述熱路中，電機中的銅耗和鐵耗是熱源，電機工作產生損耗，導致電機各部位之間，以及與外界環境之間存在溫度差△T，由於該溫度差的存在，熱量會由溫度高的地方流向溫度低的地方，即產生熱流Q 結合式( 3) 通過電路理論中的基爾霍夫電壓定律和基爾霍夫電流方程的列寫，可以求解出各熱阻上的溫差及熱流現以圖4中AB兩點為例，它們之間的溫差由兩點之間熱流Q(