基本介紹
- 中文名:阻抗變換器
- 外文名:impedance transformer
- 限制因素:工作頻帶窄
- 設計依據:切比雪夫函式
- 分類:階梯和漸變式阻抗變換器等
- 目的:改變阻抗大小和性質
簡介,主要原理,分類介紹,阻抗變換器的套用,
簡介
按結構可分為同軸線阻抗變換器、矩形波導阻抗變換器、帶狀線和微帶線阻抗變換器;按阻抗變換的規律可分為階梯阻抗變換器和漸變式阻抗變換器。階梯阻抗變換器又可分為最大平坦式及切比雪夫式阻抗變換器。
主要原理
在微波傳輸線的負載不匹配,或者不同特性阻抗的傳輸線相連時,由於產生反射,使損耗增加、功率容量減小、效率降低。為了解決這些問題,可在兩者之間連線阻抗變換器。阻抗變換器就是能夠改變阻抗大小和性質的微波元件,一般由一段或幾段不同特性阻抗的傳輸線所構成。
圖6-38是幾種單階阻抗變換器及其簡化等效電路,分別是波導型、同軸線型和微帶線型。令各種傳輸線左、右兩端的特性阻抗為Ze1、Ze2,利用λp/4阻抗變換器的特性便可實現這兩段傳輸線的匹配。λp/4阻抗變換器的特性阻抗為

這裡的波長是工作頻帶內中心頻率點所對應的波導波長。
單階阻抗變換器結構簡單,但是工作頻帶窄。為了展寬工作頻帶,可採用多階λp/4阻抗變換器。
若將多階阻抗變換器用漸變線代替,則可將工作頻帶進一步展寬。漸變線有直線式和指數式,圖6-39是微帶線指數漸變線阻抗變換器。漸變線總長l的取值取決於對頻帶低端反射係數的要求。
分類介紹
一、單節阻抗變換器
在兩段特性阻抗分別為Z01和Z02的傳輸線中間,加一段長度等於λp0/4的特性阻抗為Z0的傳輸線段,可使阻抗達到匹配。這種原理和方法適用於所有的傳輸線。對於矩形波導同樣也適用。使兩段等效阻抗不等的波導獲得匹配,即在等效阻抗分別為Z01和Z02的兩段波導中間串接一段長度為λp0/4,其等效阻抗為 的波導段即可達到。
的波導段即可達到。

對於波導寬壁尺寸口相同,窄壁尺寸分別為b1和b3的兩段矩形波導,若在它們中間加一段長度為λp0/4,波導寬壁尺寸為a,窄壁尺寸b2的波導段,則必須滿足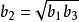
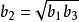
才能使兩段矩形波導獲得匹配,如圖1-22(a)所示。同理圖1-22(b)和圖1-22(c)分別表示同軸線和微帶線單節λp0/4阻抗變換器的典型結構示意圖。
二、多節λ/4階梯阻抗變換器
特性阻抗不等的兩段傳輸線相接,連線處的阻抗由於不匹配而引起反射波,而且它只有一個連線面,因此無法產生另一個反射波與原來反射波抵消。當中間加了一段λ/4阻抗變換器以後,又增加了一個連線面,這樣兩個連線面均會產生反射,而且由於兩個連線面之間有λ/4的距離,使兩個反射波到達輸入端時相位恰好相反。如果控制λ/4阻抗變換器的橫向尺寸,使兩個連線面所產生的反射波在輸入端等幅反相而抵消,則達到匹配。但因為只有兩個連線面,因此只能對一個頻率達到匹配;而且由於只有一段λ/4阻抗變換器,當要匹配兩段特性阻抗相差比較大的傳輸線時,由於兩個連線面處不連續電容比較大,會影響阻抗匹配性能。為了增加阻抗變換器的工作頻帶,以便在較寬的頻帶內具有良好的匹配性能,往往採用如圖1-23所示的多節λ/4阻抗變換器,因其形狀像階梯故又稱為多節階梯阻抗變換器。
阻抗變換器的套用
1.不同特性阻抗的傳輸線的連線
四分之一波長單節阻抗變換器的套用實例如圖3-12所示,它用來連線兩段特性阻抗分別為Z1、Z2的傳輸線。變換器的特性阻抗在同軸線情況或波導情況下變換段的尺寸。
單節變換器只能在一個頻率點上(相應於變換段電長度剛好為π/2的那個頻率)才是完全匹配的,而只在該頻率附近的一個很窄的頻帶內有近似的匹配。前面已指出,為了展寬變換器的工作頻寬,可以採用多節變換器。在N節變換器中,通過合理選擇每節的特性阻抗Zn或反射係數ρn,就可以在N個頻率點上獲得全匹配,從而使變換器總的頻帶得到增加。至於ρn的具體選擇,可以按二項式分布來確定,也可以按切比雪夫分布來確定,後者能比前者獲得更好更寬的頻寬。在多節變換器中,當把節數無限增加而保持總長度不變時,變換器由不連續的階梯過渡轉化為連續光滑變化的漸變過渡(見圖3-13),這種漸變最簡單的就是線性變化,但用指數漸變或三角函式分布漸變效果會更好。漸變段越長,匹配越好,頻寬也越寬。更為理想的是切比雪夫漸變線,將切比雪夫階梯變換器的節數無限增加而每節的長度無限縮短,使總長度不變,就得到了切比雪夫漸變變換器。在同樣長度下,這種漸變線可以做到在給定長度下反射最小;反之在給定反射下,它需要的變換段長度最短。事實上,在合理設計下,波導截面的變化,甚至軸線的變化,連續變化的性能總可以比不連續的變化好,可以說是一個普遍的規律。對阻抗變換器是如此,對上節介紹過的彎波導、扭波導等也是如此。切比雪夫函式在微波元件的設計中套用十分廣泛,不僅在阻抗變換器的設計中,也在濾波器、定向耦合器等設計中用來增加元件的工作頻率範圍。

