凸組合是一類特殊的線性組合,是若干個點的某種特定意義下的非負線性組合。
基本介紹
- 中文名:凸組合
- 外文名:convex combination
- 所屬學科:數學
- 別名:凸線性組合
- 性質:線性組合
定義
凸集聯繫






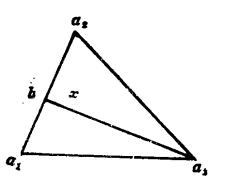
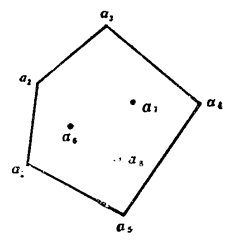
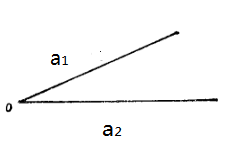
幾何意義














































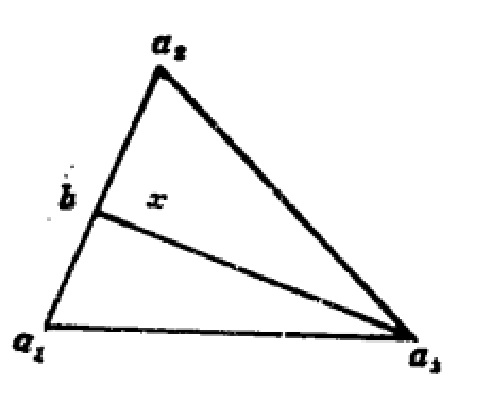
相關定理




凸組合是一類特殊的線性組合,是若干個點的某種特定意義下的非負線性組合。



























































凸組合是一類特殊的線性組合,是若干個點的某種特定意義下的非負線性組合。定義設向量 如有實數 ,且 ,則稱 為向量 的一個凸組合(凸線性組合)。凸集聯繫凸集與凸組合之間的聯繫如下:(1) 如果點 的任意凸組合仍包含在D中,...
1. 凸多邊形:延長多邊形的任意一邊為一條直線,若其餘的邊都在該直線同側,則稱之為凸多邊形。2. 凸多面體:延展多面體的任意一面為一個平面,若其餘的面都在該平面同側,則稱之為凸多面體。重要概念 直徑 這個概念適用於一般點集...
凸多面錐 凸多面錐(polyhedral cone)一類組合構形.指有限多個齊次線性不等式確定的解集.由於每一個齊次不等式的解集為E”中的半空間,所以從幾何上看,凸多面錐為有限多個半空間的交集.
凸包(Convex Hull)是一個計算幾何(圖形學)中的概念。在一個實數向量空間V中,對於給定集合X,所有包含X的凸集的交集S被稱為X的凸包。X的凸包可以用X內所有點(X₁,...Xₙ)的凸組合來構造.在二維歐幾里得空間中,凸包可想像...
局部凸空間中的緊凸集一定是其端點集的閉凸包(克賴因-米爾曼定理)。當空間是有限維時,上述結果中閉凸包可改為凸包(閔科夫斯基定理)。這一結果也就是說,緊凸集中的每一點都可用關於端點的凸組合來表示。“無限”凸組合可用關於機率...
在凸幾何中,凸集(convex set)是在凸組合下閉合的仿射空間的子集。更具體地說,在歐氏空間中,凸集是對於集合內的每一對點,連線該對點的直線段上的每個點也在該集合內。例如,立方體是凸集,但是任何中空的或具有凹痕的例如月牙形都...
在凸幾何中,凸集(convex set)是在凸組合下閉合的仿射空間的子集。更具體地說,在歐氏空間中,凸集是對於集合內的每一對點,連線該對點的直線段上的每個點也在該集合內。例如,立方體是凸集,但是任何中空的或具有凹痕的例如月牙形都...
的凸組合,所以 。而由於 是 到 的最小距離,故 根據平行四邊形定律(兩對角線的平方和等於一組臨邊平方和的兩倍),有:把(1)和(2)代入,有 故有 ,唯一性得證。在此基礎上,可以給出凸集分離定理的證明。定理證明 因為 ...
permutation and combination [數]排列組合 key combination [計]組合鍵,關鍵字組合 combination property 綜合性能 load combination 荷載組合,負載組合 convex combination [數]凸組合 combination of enterprise 企業合併 combination lock ...
在凸幾何中,凸集是在凸組合下閉合的仿射空間的子集。更具體地說,在歐氏空間中,凸集是對於集合內的每一對點,連線該對點的直線段上的每個點也在該集合內。例如,立方體是凸集,但是任何中空的或具有凹痕的例如月牙形都不是凸集。特...
在凸幾何中,凸集(convex set)是在凸組合下閉合的仿射空間的子集。更具體地說,在歐氏空間中,凸集是對於集合內的每一對點,連線該對點的直線段上的每個點也在該集合內。例如,立方體是凸集,但是任何中空的或具有凹痕的例如月牙形都...
複合透鏡(compound lens)是指兩個以上的單體透鏡構成的透鏡。用一片凸透鏡的單體透鏡也可以聚光,但為使像差儘量小,得到平衡好的清晰像,必須將各種形式及各種光學玻璃的凸透鏡和凹透鏡組合起來。將這些凹凸單體透鏡單獨或膠合組成適於...
