基本介紹
簡介,算符,交換律,廣義動量,
簡介
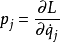
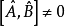

最經典的共軛物理量包括位置/動量、時間/能量等。
算符
在物理學里,算符(operator),又稱運算元,作用於物理系統的狀態空間,使得物理系統從某種狀態變換為另外一種狀態。這變換可能相當複雜,需要用很多方程來表明,假若能夠使用算符來代表,可以更為簡單扼要地表達論述。
對於很多案例,假若作用的對象有所迥異,算符的物理行為也會不同;但是,對於有些案例,算符的物理行為具有一般性,這時,就可以將論題抽象化,專注於研究算符的物理行為,不必顧慮到狀態的獨特性。這方法比較適用於一些像對稱性或守恆定律的論題。因此,在經典力學裡,算符是很有用的工具。在量子力學裡,算符為理論表述不可或缺的要素。
對於更深奧的理論研究,可能會遇到很艱難的數學問題,算符理論(operator theory)能夠提供高功能的架構,使得數學推導更為簡潔精緻、易讀易懂,更能展現出內中物理涵意。
一般而言,在經典力學里的算符大多作用於函式,這些函式的參數為各種各樣的物理量,算符將某函式映射為另一種函式。這種算符稱為“函式算符”。在量子力學里的算符稱為“量子算符”,作用的對象是量子態。量子算符將某量子態映射為另一種量子態。
交換律
交換律(Commutative property)是被普遍使用的一個數學名詞,意指能改變某物的順序而不改變其最終結果。交換律是大多數數學分支中的基本性質,而且許多的數學證明需要倚靠交換律。簡單運算的交換律許久都被假定存在,且沒有給定其一特定的名稱,直到19世紀,數學家開始形式化數學理論之後,交換律才被聲明。
