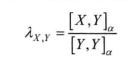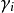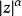共變

根據統計信號分析的二階矩理論，兩個隨機變數的協方差的概念是十分重要的。實際上，信號預測理論，濾波理論，平滑理論以及大多數信號處理的統計理論和方法都是建立在協方差基礎上的。

然而，由於SαS分布沒有有限的方差，所以不存在協方差。於是，一個稱為共變(Covariation)的概念於1978年由Miller提出。共變這個量在SαS分布隨機變數中的地位與協方差在高斯分布隨機變數中的地位相似。

基本介紹

• 中文名：共變
• 外文名：Covariation
• 所屬類型：數學術語
• 提出時間：1978年
• 提出者：Miller

定義介紹

若X和Y為聯合SαS分布隨機變數，特徵指數l<α≤2，則其共變定義為

式中：S為單位圓：m(·)為SαS分布隨機變數(X，Y)的潛測度：符號“ <·>”表示運算=sign(z)。復值SαS分布隨機變最具有相似的共變定義。

隨機變數X與Y的共變係數(Covariation Coefficient)定義為

由此可知，共變與協方差的主要區別在於共變沒有對稱性(α=2除外)，即

由於潛測度不易計算，因此基於共變定義的計算方法缺乏實用性。在實際套用中，通常基於共變、共變係數與分數低階矩之間的關係定理（見下文），從而使共變成為具有實用價值的概念。

相關性質定理

定理 具有聯合SαS分布的隨機變數X和Y，滿足1<a≤2，假定Y的分散係數為，則

下面給出有關共變的基本性質.

性質1 共變]對於X是線性的。如果X1，X2，Y服從聯合SαS分布，則

對任意實常數A和B都成立。

性質2 當α=2時，即當X,Y服從零均值聯合高斯分布，則X和Y的共變就退化為X和y的協方差

性質3 一般來說，對於第二個變數Y不是線性的。但是，它對於Y存在下面的偽線性：即如果Y1，Y2是獨立的，且X，Y1，Y2服從聯合SαS分布，則

對任意實常數A和B都成立。

性質4 如果X,Y是獨立的且服從聯合SαS分布，則

但是反之通常是不成立的。

性質5 對於任意的聯合SαS隨機變數，有如下式所示的柯希一許瓦茲不等式成立

特別地，如果X，Y的分散係數為1，則有

通常，兩個SαS隨機變數X和Y的共變很難進行解析計算。而當X和Y均為獨立SαS隨機變數的線性組合時，則是一個例外。利用共變的基本性質，容易得到下面的命題

命題 1 設Ui是獨立的SαS隨機變數，其分散係數為，i=1，…，n。若對於任意的數a1，......，an，b1，......,bn，其中所有的bi都是非零的，有如下關係

則