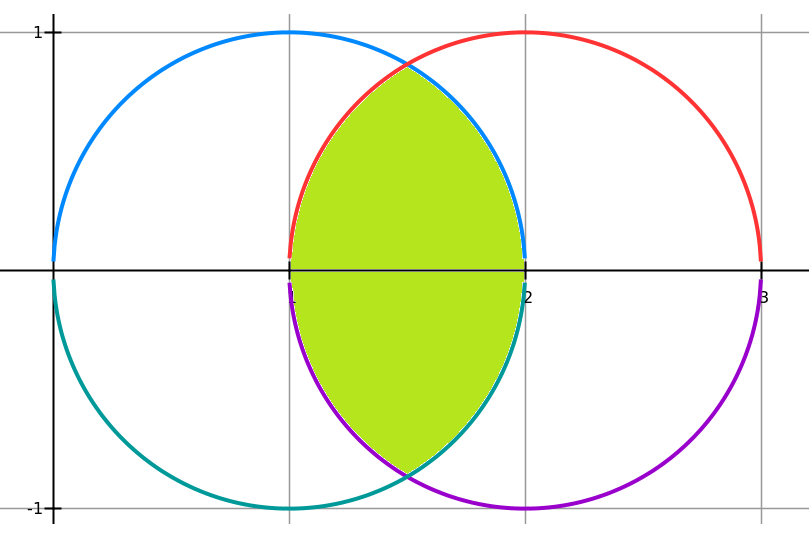
兩圓相交(intersection of two circles)兩圓間的一種位置關係.指兩圓有兩個公共點。
兩圓相交(intersection of two circles)兩圓間的一種位置關係.指兩圓有兩個公共點。釋義兩圓相交的充分必要條件是:圓心距小於兩圓半徑的和，而大於兩圓半徑的差的絕對值.如上圖，00，與00:的半徑分...
相交是指兩圓有多於一個交點。相容是指兩圓沒有交點且一個圓在另一個內部。兩個圓相交若且唯若兩個圓心之間的距離嚴格小於兩圓的半徑之和，並嚴格大於兩圓的半徑之差。判別方法 在平面解析幾何中，設兩條直線的方程為：那么 相交...
兩球相交(intersection between two spheres )兩球間的一種特殊位置關係，指不重合的兩球面至少有兩個公共點的位置關係。這時交集是一個圓周，該圓周所在平面垂直於兩球的連心線，且圓心在兩球的連心線上.（如兩球半徑分別為R與r(R)...
圓-圓定位 圓-圓定位是2020年公布的測繪學名詞。定義 以測點至兩個已知點的距離為半徑，已知點為圓心，兩圓相交確定點位的方法。出處 《測繪學名詞》。
當兩個圓相交時，兩個交點的連線叫公共弦。性質 兩圓心所在直線垂直平分公共弦。相交兩圓的公共弦所在的直線方程 若圓C1：x²+y²+D₁x+E₁y+F₁=0與圓C2：x²+y²+D₂x+E₂y+F₂=0相交 則公共弦的直線...
公切線的性質是一個數學概念。兩圓內含時沒有公切線，兩圓內切時有且只有一條公切線，兩圓相交時有兩條公切線，兩圓外切時有三條公切線，兩圓相離時有四條公切線。若兩圓有兩條外公切線，那么這兩條外公切線長相等；若兩圓有兩...
圓周角(angle of circumference)是指頂點在圓上，且兩邊和圓相交的角。在同圓或等圓中，兩圓周角相等，則其所對的弦(或弧)也相等；反之，等弧所對的圓周角相等。而等弦所對圓周角相等或相補，圓周角的度數等於它所對弧的度數的...
交角指的是線與線、線與面或面與面相交而成的角。廣義交角 jiāojiǎo [corner] 線與線、線與面或面與面相交而成的角 圓的交角 兩個圓相交，兩圓在交點處的切線會形成夾角，這個夾角稱為交角。很小的一段弧可以近似看作圓在...
倍弦（multiple chord ）是平面幾何術語，是與相交圓有關的的一種特殊弦，過兩圓交點的直線被兩圓截得的部分叫做倍弦。基本介紹 倍弦是一種特殊弦，指與相交兩圓有特定位置關係的線段。如圖1所示，若兩圓相交，過一交點引直線與兩...
密克定理是幾何學中關於相交圓的定理。1838年，奧古斯特·密克（Auguste Miquel）敘述並證明了數條相關定理。許多有用的定理可由其推出。定理：設在一個三角形的每一邊上取一點，過三角形的每一頂點與兩條鄰邊上所取的點作圓，則這三...
兩圓相交，則有2條公切線（外切）；若兩圓內切，則有1條公切線；若兩圓內含，則有0條公切線。尺規作圖方法 方法一：平移法（如圖2所示）取圓O₁，圓O₂上的半徑O₁A，O₂B；以B為圓心，以O₁A的長度為半徑畫圓交...
∴ △PBT∽△PTA(兩角對應相等，兩三角形相似)；∴PB：PT=PT：AP；即：PT²=PB·PA。例題解析 【例1】求證：兩個相交圓的公共弦的延長線上任何一點到兩圓的切線等長（如圖2）。已知：P為兩圓公共弦BA的延長線上任意一點，和 ...
若點在圓上，則冪為0；若點在圓內，則冪為負數，其絕對值等於過點 且垂直於 的弦長的一半的平方。根軸 平面上兩不同心的圓 顯然，對兩圓等冪的點集是直線：該直線稱為兩圓的根軸。根軸必垂直於兩圓的連心線。若兩圓相交，...
(4)如果兩圓相交,那么連線兩圓圓心的線段(直線也可)垂直平分公共弦。 (5)弦切角的度數等於它所夾的弧的度數的一半。 (6)圓內角的度數等於這個角所對的弧的度數之和的一半。 (7)圓外角的度數等於這個角所截兩段弧的度數之差的一...
d>r，則直線與圓相離；d=r，則直線與圓相切；d 兩圓位置關係 若兩圓的方程分別為C₁： ，C₂： ：則兩圓外離 ；兩圓外切 ；兩圓相交 ；兩圓內切 ；兩圓內含 .一般式 此方程可用於解決兩圓的位置關係：配方化...
1.若直徑為BC，CA，AB的圓分別與直徑為AX，BY，CZ的圓相交，則諸交點共圓或共線。如圖1中以BC，AX為直徑的兩圓交於L，M兩點；以AC，BY為直徑的兩圓交於N，O兩點；以AB，CZ為直徑的兩圓交於P，Q兩點，則L，M，N，O，P...
(1)(2)聯立的解，是兩圓的公共點M(x₁,y₁)，N(x₂,y₂)。如果是兩組不等實數解，MN不重合且兩圓相交，根軸是兩圓的公共弦。如果是相等實數解，MN重合，兩圓相切，方程表示兩圓的內公切線。如果是共軛虛數解，兩圓...
④兩相切圓的連心線過切點。（連心線：兩個圓心相連的直線）⑤圓O中的弦PQ的中點M，過點M任作兩弦AB，CD，弦AC與BD分別交PQ於X，Y，則M為XY之中點。（4）如果兩圓相交，那么連線兩圓圓心的線段（直線也可）垂直平分公共弦。...
與多邊形各頂點都相交的圓叫做多邊形的外接圓。幾何圖形在圓內,而其向頂點在此圓周上 內切圓 與多邊形各邊都相切的圓叫做多邊形的內切圓。圓在幾何圖形內,圓周與外側幾何圖形的邊（或圓周）相切。辨析 關於內切圓和外切圓：只有兩圓...
②一條邊與圓周相交，另一條邊與圓相切，切點在圓周上；③弦切角的大小等於它所夾的弧所對的圓心角的大小的一半。弦切角定理 弦切角等於它所夾的弧所對的圓周角。推論1：弦切角等於它所夾的弧所對的圓心角的一半。推論2：兩個弦切角...
若兩圓的圓心的距離是d，大圓半徑是R，小圓半徑是r。則內切可以表述為d=R-r。 相反地，外切可以表述為d=R+r。圓與圓的位置關係 相離（d＞R+r），外切（d=R+r），相交（d＜R+r），內切（d=R-r），內含（d＜R-r）
解：∵AC、BC是⊙O的兩條切線 ∴AC=BC（切線長定理）∴∠CAB=∠CBA（等腰三角形中等邊對等角）【例2】如圖5，AD是ΔABC中∠BAC的平分線，經過點A的圓與BC相切於點D，與AB，AC分別相交於E，F.求證：EF//BC.證明：連線DF ...
