全等球面三角形

全等球面三角形(congruent spherical triangles)是指兩個球面三角形的一種等價關係，即在同球面或等球面上，一個球面三角形的三邊、三角分別與另一個球面三角形的三邊、三角對應相等的兩個球面三角形。

基本介紹

• 中文名：全等球面三角形
• 外文名：congruent spherical triangles
• 所屬學科：數學
• 所屬問題：球面幾何
• 簡介：兩個球面三角形的一種等價關係

基本概念

全等球面三角形：（1）在同一球或等球面上，若兩球面三角形的邊及角分別對應相等，且排列順序一致時，則稱這兩個球面三角形為全等。

（2）全等球面三角形指在同球面或等球面上，一個球面三角形的三邊、三角分別與另一個球面三角形的三邊、三角對應相等的兩個球面三角形。全等球面三角形可分為兩類：1.定向相同的(稱為本質相等的球面三角形或絕對相等的球面三角形)；2.定向相反的(稱為鏡像相等的球面三角形)。

以上兩個定義第（1）個定義實際上是第（2）個定義中的絕對相等的球面三角形，有的書籍上是第（1）種定義，有的書籍上是第（2）種定義。

一般所說全等球面三角形指的是第（1）種定義中所說的情形。

球面三角形全等的條件

在同球面或等球面上，具備下列條件之一的兩個球面三角形全等：

1) 兩角及其夾邊對應相等。

2) 兩邊及其夾角對應相等。

3) 兩角及其中一角的對邊對應相等，且其他兩角的對邊都小於一象限，或都大於一象限。

4) 兩邊及其中一邊的對角對應相等，且其他兩邊的對角均為銳角，或均為鈍角。

5) 三邊對應相等。

6) 三角對應相等。

詳細介紹

對稱球面三角形是全等球面三角形

如圖1，設在同一個球面上兩個三角形ABC和A'B'C'關於大圓l對稱，那么大圓弧AA'被大圓l垂直平分。

不難看出：A和A'關於l所在平面成鏡面反射。同樣地，B和B'，C和C'都關於I所在平面成鏡面反射。

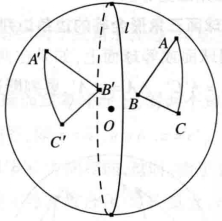圖1

如果以球心O為端點，連線OA，OB，OC作三條射線，就可以得到一個類似於三稜錐O-ABC形狀的“空間角”，它由三稜錐的三個側面圍成，我們把它稱為三面角，記為三面角O- ABC，同樣方法還可以得到三面角O-A'B'C'。 因此，三面角O-ABC與三面角O-A'B'C'也關於l所在平面成鏡面反射。所以，它們的三個面上的平面角分別相等。

即：∠AOB=∠A'OB'，

∠COA=∠C'OA'，

∠BOC=∠B'OC'，

由此得到a=a'，b=b'，c=c'。

這兩個三面角的三個二面角也分別相等，由此得到：

∠A=∠A'，∠B=∠B'，∠C=∠C'，

因此，球面三角形ABC全等於球面三角形A'B'C'，記為：

△ABC≌A'B'C'。

於是：

同一球面上，對稱的兩個球面三角形也是全等的三角形。

全等球面三角形的邊角邊判定定理

在平面上，如果兩個三角形中，有兩組對邊及其夾角對應相等，那么這兩個三角形全等。這是平面幾何關於兩個三角形全等的判定定理。球面幾何是否也有類似的結論?答案是肯定的。

在同球面或等球面上，如果兩個球面三角形的兩組對邊及其夾角對應相等,那么這兩個球面三角形全等。

這個性質稱為兩個球面三角形全等的邊角邊判定定理。

如圖2，設在同球面或等球面上，如果在兩個球面三角形ABC和A'B'C'中，AB=A'B'，AC=A'C'，∠A=∠A’，要判斷這兩個球面三角形是否全等，可以用重合法。

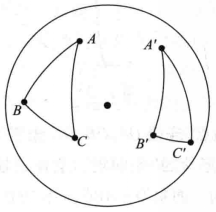圖2

我們在平面幾何里也常用重合法進行證明，就是通過移動把一個圖形轉移到與另一個圖形重合的位置，從而得到所需的結論。平面幾何運用重合法的依據，是平面的對稱性。因為球面和平面的對稱性類似，在球面幾何中，也可以用重合法進行證明。

利用球面的對稱性，根據AB =A'B'，可以移動球面三角形A'B'C'，使A'B'落在AB的位置，弧的端點A'與A重合，B'與B重合。

這時,大圓AB把球面分成兩半，這就看C'落在哪個半球上，再分成兩種情況分別討論。

(1)若C'落在包含C的半球面內，由於∠A=∠A'，可知大圓弧A'C'落在AC上，又AC=A'C'，所以C'落在C上。因而球面三角形A'B'C'的新位置與球面三角形ABC重合,所以這兩個球面三角形全等。

(2)若C'落在另外的半球面上,那么利用類似(1)的理由，可知球面三角形A'B'C'的新位置與球面三角形ABC對稱，所以這兩個球面三角形全等。

全等球面三角形的邊邊邊判定定理

平面上三邊對應相等的兩個三角形全等，球面三角形是否也有這樣的性質?

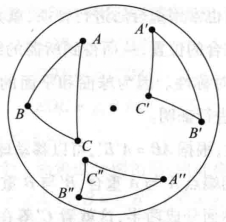圖3

如圖3，設在同球面或等球面上，有兩個球面三角形ABC和A'B'C'，它們的三對對應邊相等，即a=a',b=b',c=c'。

(1)如果三角形ABC與A'B'C'方向相同，這時,由於它們在同球面或等球面上，所以可以通過移動使A與A'重合，C與C'重合，自然B與B'重合。由於a=a',b=b'，所以C與C'一定重合。因此，這兩個球面三角形可以完全重合。

(2)如果△ABC與A'B'C'方向不相同，如圖3，先作△ABC的球面對稱三角形A"B"C"，由球面對稱三角形的性質,有：

△ABC≌△A"B"C"。

這時，△A"B”C"與△A'B'C'方向相同且對應邊相等，所以△A"B"C"≌△A'B'C'即△ABC≌△A'B'C'。

也就是說：

在同球面或等球面上，如果兩個球面三角形的三對對應邊相等，那么這兩個球面三角形全等。

這個性質稱為兩個球面三角形全等的邊邊邊判定定理。

全等球面三角形的角邊角判定定理

此外，我們還有如下性質:

在同球面或等球面上，如果兩個球面三角形的兩對對應角和它們的夾邊對應相等，那么這兩個球面三角形全等。

這個性質稱為兩個球面三角形全等的角邊角判定定理。

此定理的證明也可以用重合法證明，讀者可以試一試。

通過上面的討論，我們會發現，平面上兩個三角形全等的概念及判定全等的邊角邊定理，邊邊邊定理，角邊角定理都可以推衍到球面上，但是要注意，這些概念和性質只能在同--球面或半徑相等的球面上討論，只有滿足這一條件，上述判定定理才能成立。

全等球面三角形的角角角判定定理

國中老師在學習平面幾何時，常常要提醒“如果兩個三角形的三組對應角相等，只能判斷它們相似，但不一定全等”；而球面上，我們卻可以大大方方地把“不”字去掉，因為我們可以用極三角形性質，嚴格證明如下的結論：

在同球面或等球面上，如果兩個球面三角形的三組對應角對應相等，那么這兩個球面三角形全等。

這個性質稱為兩個球面三角形全等的角角角判定定理。

從以上討論可以看到，球面三角形全等和平面三角形全等雖然有很多性質都相同，比如角邊角、邊角邊、邊邊邊判定定理。但是球面三角形全等卻增加了一個角角角判定定理，這個定理在平面幾何中只能作為兩個三角形相似的判定定理。球面上的幾何和平面上的幾何存在很多相似之處，但也存在著巨大差別。