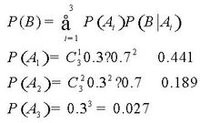全機率公式

全機率公式為機率論中的重要公式，它將對一複雜事件A的機率求解問題轉化為了在不同情況下發生的簡單事件的機率的求和問題。

內容：如果事件B1、B2、B3…Bn 構成一個完備事件組，即它們兩兩互不相容，其和為全集；並且P（Bi)大於0，則對任一事件A有

P(A)=P(A|B1)P(B1) + P(A|B2)P(B2) + ... + P(A|Bn)P(Bn)。

或者：p(A)=P(AB1)+P(AB2)+...+P(ABn))，其中A與Bn的關係為交)。

基本介紹

• 中文名：全機率公式
• 外文名： Total Probability Theorem
• 簡介：機率論中的重要公式
• 屬性：數學理論
• 範圍：機率論

定義

定理

若事件A1，A2，…構成一個完備事件組且都有正機率，則對任意一個事件B，有如下公式成立：

P(B)=P(BA₁)+P(BA₂)+...+P(BA_n)=P(B|A₁)P(A₁) + P(B|A₂)P(A₂) + ... + P(B|A_n)P(A_n).

此公式即為全機率公式。

特別地，對於任意兩隨機事件A和B，有如下成立：

其中A和Ac為對立事件。

套用舉例

我們來看一個簡單的例子：

例：高射炮向敵機發射三發炮彈，每彈擊中與否相互獨立且每發炮彈擊中的機率均為0.3，又知敵機若中一彈，墜毀的機率為0.2，若中兩彈，墜毀的機率為0.6，若中三彈，敵機必墜毀。求敵機墜毀的機率。

解：設事件B=“敵機墜毀”；Ai=“敵機中彈”；i=0,1,2,3

實際上我們從題目知道應該是A0,A1,A2,A3構成完備事件組，但是敵機墜毀只和A1,A2,A3有關，即
，則我們可用如下公式：

全機率公式和Bayes公式

機率論的一個重要內容是研究怎樣從一些較簡單事件機率的計算來推算較複雜事件的機率，全機率公式和Bayes公式正好起到了這樣的作用。對一個較複雜的事件A，如果能找到一伴隨A發生的完備事件組B1、B2```，而計算各個B的機率與條件機率P(A/Bi)相對又要容易些，這是為了計算與事件A有關的機率，可能需要使用全機率公式和Bayes公式。