基本介紹
- 中文名:全模型
- 外文名:Full Model
- 別稱:飽和模型
- 簡介:包含所有自變數的線性回歸模型
- 所屬學科:數學
- 所屬問題:數理統計
基本介紹
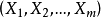
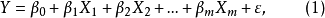
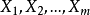

自變數選擇對估計和預測的影響
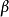
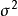
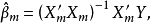
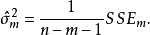
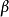
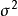
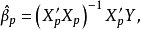
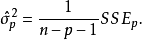
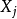
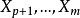
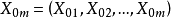
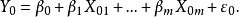
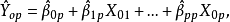
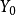
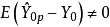
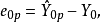
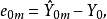
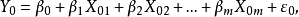
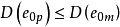
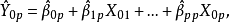
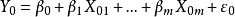
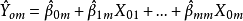

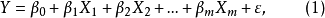
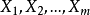
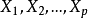

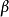
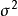
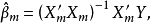
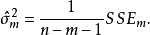
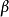
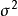
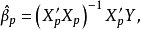
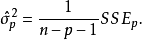
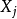
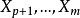
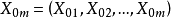
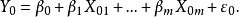
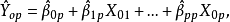
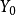
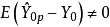
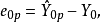
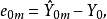
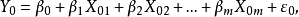
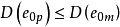
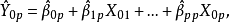
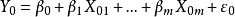
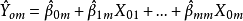
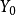
全模型(Full Model)也稱為飽和模型(Saturated Model),指包含所有自變數的線性回歸模型。在對回歸模型進行一般線性檢驗時,需要先擬合一個全模型,並計算其殘差平方和...
《全模型軟體系統設計》的內容分為兩部分:人機界面部分的設計和非人機界面部分的設計。人機界面部分的設計主要介紹的是如何完成人與機器之間互動的設計;非人機界面...
北京皇城全景模型是北京皇城藝術館記憶體放的一座反映明清北京皇城風貌的全景沙盤。面積為三十多平方米。...
《壓力容器全模型ANSYS分析與強度計算新規範》是2012年6月出版的圖書,作者是欒春遠。...
中文名稱 全球模型 英文名稱 global model 定義 雖然不是面面俱到而是針對特定的地理過程的,但在空間上包含了整個地球區域的模型。 套用學科 地理學(一級學科)...
全腦模型(Whole Brain Model)是由20世紀70年代,擔任GE管理髮展中心主任的奈德·赫曼(Ned Herrmann)博士,對自己集音樂家、藝術家、科學家的興趣感到好奇。因而投入...
或稱理想混合模型。是化工過程設備模擬中常用的模型。全混流是理想流動的一種。其特徵是在連續流動過程中,無論軸向或是徑向都是達到完全混合,以致物系參數均一。...
通過主觀意識藉助實體或者虛擬表現構成客觀闡述形態結構的一種表達目的的物件(物件並不等於物體,不局限於實體與虛擬、不限於平面與立體)。模型≠商品。任何物件定義為...
全信息對象指包含空間、時態和屬性信息的土地對象。全信息對象模型即是運用面向對象的設計方法,將土地現象和過程的空間與屬性信息隨時間的變化封裝成由時態版本組成的...
2.0+移動互聯的全數字時代,用戶行為\消費觸點變革為SICAS模型1,即:Sense— Interest&Interactive—Connect&Communicate—Action—Share (品牌與用戶相互感知— 產生興趣...
MA模型(moving average model)滑動平均模型,模型參量法譜分析方法之一,也是現代譜估中常用的模型。q階移動平均模型的自相關係數q階截尾,偏自相關係數拖尾。...
哈夫機率模型基本法則依然是引用萬有引力原理。它提出了購物場所各種條件對消費者的引力和消費者去購物場所感覺到的各種阻力決定了商圈規模大小的規律。哈夫模型區別於...
日本經濟學家濱田宏一(Y.Hamada)提出的哈馬達模型和羅格夫建立的羅格夫模型是對國際貨幣政策協調效應進行分析的兩個著名的理論模型。...
經濟訂貨批量模型,又稱整批間隔進貨模型EOQ模型, 是目前大多數企業最常採用的貨物定購方式。該模型適用於整批間隔進貨、不允許缺貨的存儲問題,即某種物資單位時間的...
全球發展模型(global development model),亦稱“整體模型”或“全球模型”。根據對應、模擬的原理和方法, 反映全世界今後各主要方面發展過程和前途的預測。福萊斯坦...
Logit模型(Logit model),也譯作“評定模型”,“分類評定模型”,又作Logistic regression,“邏輯回歸”,是離散選擇法模型之一,Logit模型是最早的離散選擇模型,也是...
全面客戶滿意模型就是以客戶全程體驗為基礎的滿意度研究。通過分析客戶與企業在產品、服務等各個方面的接觸點以及客戶的全程體驗滿意度,發現影響顧客滿意度的因素、...
全尺寸是指1:1比例,全尺寸油泥模型就是指與真車尺寸一樣,模型的輪廓曲線和尺寸都是按照嚴格的要求製作出來,設計人員可以對車身表面的細節部分進行比較和修改,設計...
模型是指對於某個實際問題或客觀事物、規律進行抽象後的一種形式化表達方式。模型結構是指為解決某種問題而創建的模型自身各種要素之間的相互關聯和相互作用的方式,...
風控模型,是風險控制模型的簡稱。常見於信貸擔保公司,用來對業務進行風險控制。風控模型當下國內主要有:工商銀行開發的風控模型。...
層次模型是指用一顆“有向樹”的數據結構來表示表示各類實體以及實體間的聯繫,樹中每一個節點代表一個記錄類型,樹狀結構表示實體型之間的聯繫。層次模型是最早用於...
Est模型基本信息 編輯 要想達到這個目標,必須將目標定位於特定的顧客群體,找到一個適合自己的Est定位,並努力在這方面做得最出色。作者說的定位,即確定目標顧客,並...
高達模型(gunpla—gundam plastic model)一直是高達動畫周邊系列不可動搖的主導產品, 高達模型的出現將動畫上的巨大的機器人立體化地展現。1980 年,萬代將出現在高達...
在粒子物理學裡,標準模型(英語:Standard Model, SM)是一套描述強力、弱力及電磁力這三種基本力及組成所有物質的基本粒子的理論。它隸屬量子場論的範疇,並與量子...
又稱材料的力學本構方程,或材料的應力-應變模型。描述材料的力學特性 (應力-應變-強度-時間關係)的數學表達式。材料的應力-應變關係是很複雜的,具有非線性,粘彈...
全微縮是以全景、全時、全維”的模型製作手法,演繹城市人文變遷。...... 全微縮是以全景、全時、全維”的模型製作手法,演繹城市人文變遷。 [1] ...
