全對偶整數性(total dual integrality)組合最佳化問題的一種性質。指線性規劃max Z=c,滿足Ax=b具有如下性質:矩陣A及向量b均取整數值,而且對於任意的整數向量。此問題的對偶問題均具有整值最優解。
基本介紹
- 中文名:全對偶整數性
- 外文名:total dual integrality
- 分類:性質
- 屬性:數學術語
- 相關:最優解
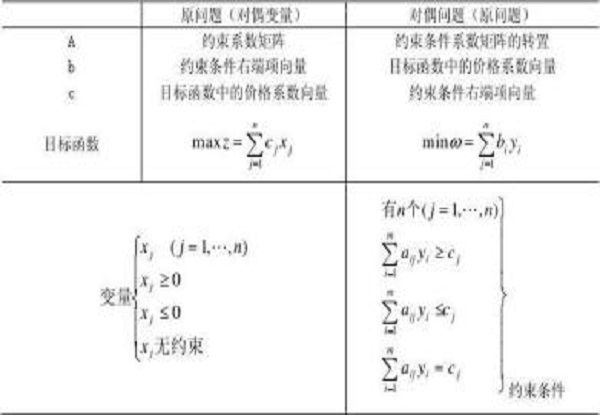
全對偶整數性(total dual integrality)組合最佳化問題的一種性質。指線性規劃max Z=c,滿足Ax=b具有如下性質:矩陣A及向量b均取整數值,而且對於任意的整數向量。此問題的對偶問題均具有整值最優解。
全對偶整數性(total dual integrality)組合最佳化問題的一種性質。指線性規劃max Z=c,滿足Ax=b具有如下性質:矩陣A及向量b均取整數值,而且對於任意的整數向量。此問題的對偶問題均具有整值最優解。...
全對偶整數性(total dual integrality)組合最佳化問題的一種性質。指線性規劃max Z=c,滿足Ax=b具有如下性質:矩陣A及向量b均取整數值,而且對於任意的整數向量。此問題的對偶問題均具有整值最優解。簡介 由此性質可知,約束條件Ax=b決定的多面形的所有頂點均為整點。因此,對組合最佳化問題而言,全對偶整數性是一個...
反交鎖多面形(anti-blocking polyhedra)一類特殊的多面形.類似於線性規劃的對偶約束,設B0 _勺E E+ I獷}A簇‘}.此多面形稱為反交鎖多面形.在交鎖多面形與反交鎖多面形之間具有良好的對偶性質,而且具有全對偶整數性.若干組合最佳化問題,如匹配問題、網路上最大流問題等,可歸結為建立在交鎖多面形上的最佳化...
第4 章三角形覆蓋的全對偶整數性. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 4.1 概況. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ...
