含義及計算
含義
內部一致性信度(internal consistency reliability),也叫做內部一致性係數(coefficient of internal consistancy)、
同質性信度(homogeneity reliability),它是指測驗內部所有題目間的一致性程度。
這裡的“一致性”指的是分數的一致,而非題目內容或形式的一致。因此,若測驗的各個題目得分有較高的正相關時,不論題目內容和形式如何,測試都是同質的;相反,即使所有題目看起來都好像測量同一特質,但分數相關很低時,這個測驗就是
異質的。
內部一致性信度主要反映的是測驗內部題目之間的
信度關係,考察測驗的各個題目是否測量了相同的內容或特質。
說明
複本法適用於許多測驗,尤其是
能力測驗(學業能力,智力,特殊能力)。但是,為測驗建立複本通常花費較高,而且很難順利編制。於是,研究者就把測驗項目劃分成不同的樣本,從而間接地考慮一致性信度,這就是內部一致法(method of internal consistency)。
但是,內部一致性係數(internal consistency coefficients)並不能反映這些誤差。因此,不能把內部一致性係數等同於真正的
重測信度或
複本信度。
計算
基本公式
測量同質性的基本公式如下:
其中K為構成測驗項目數,
為項目間相關係數的平均數,
為同質性信度值。
庫—理信度係數
庫德(G. F. Kuder)和
理查遜(M. W. Richardson)提出了一系列公式來估計測驗的信度,但只適用於答對一題得一分、答錯無分的測驗。
1)K-R20公式:
式中K表示構成測驗的題目數,pi為通過第i題的人數比例,qi為未通過第i題的人數比例, 為測驗總分的變異數。
2)K-R21公式:
式中K為構成測驗的題目數,
為測驗總分的平均數,
為測驗總分的變異數。
克倫巴赫α係數
針對項目多重記分的測驗,克倫巴赫(L. J. Cronbach)提出
α係數的方法,其公式為:
式中K為測驗的題目數,
為某一題目的變異數,
為測驗總分的變異數。
克倫巴赫α係數是學術界普遍使用內部一致性
係數(Cronbachα)檢驗量表的內部一致性信度。Hair,Anderson,Taehan,eta1.(1988)指出,內部一致性係數大於0.7表明量表的可靠性較高;在探索性研究中,內部一致性係數可以小於0.7,但應大於0.6;Peter(2002)指出,問項數量小於6個時,內部一致性係數大於0.6,表明量表是有效的。本研究利用各個
潛變數的Cronbachα係數處於0.793~0.931(見下表),都超過了0.7可接受水平,表明各個概念的量表都具有較高的可靠性。
 相關書籍
相關書籍各概念量表Cronbachα係數
量表名稱 | 問項數 | Cronbachα係數 |
PM | 3 | 0.909 |
NM | 4 | 0.907 |
MMM | 4 | 0.931 |
MRM | 3 | 0.913 |
BR | 3 | 0.793 |
SC | 3 | 0.820 |
UR | 4 | 0.804 |
PL | 4 | 0.892 |
AR | 4 | 0.899 |
荷伊特信度
1941年荷伊特(C. Hoyt)提出用分差分量比來衡量測驗內部一致性的方法,公式如下:
rxx=1-MS人×題/MS人
式中MS人是同人與人間差別有關的均方差,MS人×題是同人與題目互動作用有關的均方差。
因素分析
有些測量學家認為
因素分析是決定測驗同質性的最好方法,特別是當測驗明顯測量的是幾個不同的特質時,其具體方法如下:
先建立每個被試在每個題目上得分的資料矩陣,再建立所有題目間的相關矩陣,然後對每一組有相關的題目命名一個因素。
現在,一般研究人員只需掌握因素分析法的基本原理,藉助計算機進行演算,並能對計算機運算後輸出的結果進行解釋就可以了;無需耗費時間和精力在算數演練上。
綜合信度ρo係數分析
另一種評價內部一致性信度的方式是利用各個
潛變數的綜合信度ρ
o係數,具體可接受的標識綜合信度ρ
o係數是0.7(Chin,1988;Barclay,Higgins,&Thompson,1995)。從下表可以看出,綜合信度ρ
o係數為0.740~0.905,均超過了0.7可接受水平。
潛變數 | 觀測變數 | 標準化路徑係數 | T值 | 綜合信度ρo係數 | AVE值 |
PM | PM1 | 0.85 | 0.881 | 0.712 | |
PM2 | 0.80 | 16.58 | | |
PM3 | 0.88 | 18.82 | | |
NM | NM1 | 0.79 | | 0.0904 | 0.702 |
NM2 | 0.87 | 17.27 | | |
NM3 | 0.85 | 16.75 | | |
NM4 | 0.84 | 16.55 | | |
MMM | MMM1 | 0.78 | 0.894 | 0.677 | |
MMM2 | 0.86 | 16.57 | | |
MMM3 | 0.84 | 16.10 | | |
MMM4 | 0.81 | 15.40 | | |
MRM | MRM1 | 0.85 | | 0.904 | 0.736 |
MRM2 | 0.91 | 20.48 | | |
MRM | 30.85 | 18.74 | | |
BR | BR1 | 0.77 | | 0.815 | 0.668 |
BR2 | 0.83 | 14.15 | | |
BR3 | 0.71 | 12.19 | | |
SC | SC1 | 0.81 | | 0.848 | 0.783 |
SC2 | 0.83 | 15.27 | | |
SC3 | 0.78 | 14.44 | | |
UR | UR1 | 0.76 | | 0.833 | 0.556 |
UR2 | 0.79 | 13.26 | | |
UR3 | 0.72 | 12.19 | | |
UR4 | 0.71 | 12.00 | | |
PL | PL1 | 0.79 | | 0.905 | 0.706 |
PL20.90 | 18.06 | | | |
PL3 | 0.91 | 18.33 | | |
PL4 | 0.75 | 14.33 | | |
AR | AR1 | 0.77 | | 0.891 | 0.671 |
AR2 | 0.91 | 17.17 | | |
AR3 | 0.81 | 15.36 | | |
AR4 | 0.78 | 14.59 | | |
IB | IB | 0.86 | | 0.740 | 0.740 |
註:*表示該數值在計算過程被設定為1,因此沒有T值。
從上述兩方面的信度指標分析結果來看,所有概念的量表都滿足最低要求,這充分說明本研究所使用的量表具有良好的內部一致性信度。
存在的問題
內部一致性估計是有用的信度
量數,因為它只測量一次,因此可以排除記憶和練習的效果。然而,也存在一定的問題:
1)它們只可在測量單一特質的測驗上使用。
e.g.它們可用於拼音測驗,但不能用在包含拼音、閱讀理解和作文等部分的語文測驗。
2)當套用在速度測驗上時,內部一致性量數會有信度估計膨脹的現象。
因為速度測驗都是簡單或相對簡單的題目,並且要在限制時間內完成。在這樣的測驗中,受測者應該可以答對他所作答的大多數題目,因此內部一致性都會很高。




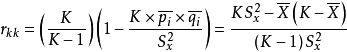
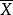

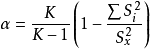



 相關書籍
相關書籍