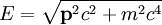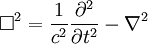相關詞條
- 克萊因-高登方程
克萊因-高登方程(Klein-Gordon equation)是相對論量子力學和量子場論中的最基本方程,它是薛丁格方程的相對論形式,用於描述自旋為零的粒子。克萊因-高登方程是由瑞典...
- 狄拉克方程
為了避免克萊因-高登方程中機率不守恆的問題,狄拉克在假設方程關於時間與空間的微分呈一次關係後得出了有名的狄拉克方程。但該方程仍無法避免得出負能量解的問題。...
- 負能態
狄拉克方程卻自動地導出這些重要基本性質,是理論上的重大進展。為了避免克萊因-高登方程中機率不守恆的問題,狄拉克在假設方程關於時間與空間的微分呈一次關係後得出了...
- 狄拉克空穴理論
1928年建立的相對論電子波動方程(也稱狄拉克方程)就是經過對薛丁格方程和克萊因-高登方程進行改造而得到的。這一新的數學模型的建立大大地豐富了現代人的時空觀和...
- 拉普拉斯運算元
達朗貝爾運算元通常用來表達克萊因-高登方程以及四維波動方程。參考資料 1. 王元,文蘭,陳木法.數學大辭典:科學出版社,2010 詞條標籤: 科學百科數理科學分類 , 科學,...