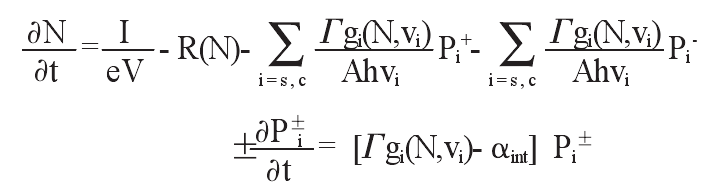光學邏輯

光邏輯門是實現高速光分組交換、全光地址識別、數據編碼、奇偶校驗、信號再生、光計算和未來高速大容量全光信號處理的關鍵器件，同時，光邏輯門的發展是實現電計算向光計算跨越的橋樑，可以突破“電子瓶頸”的限制，提高網路容量，實現全光3R再生。

基本介紹

• 中文名：光學邏輯
• 外文名：optical logic
• 學科：計算機科學與技術
• 主要體現：光邏輯門
• 功能：高速光分組交換、全光地址識別等
• 材料：半導體光放大器

基本概念

在未來的全光網路中，光交換、光計算和光傳輸是實現全光信號處理的核心單元，而它們都要以全光邏輯門為基礎工作。光交換可以分為光線路交換、光突發交換和光分組交換，光邏輯門是實現光交換系統的核心器件和決定網路性能的關鍵因素，光交換技術的最終發展趨勢是光控光交換，因此，實現光分組交換的關鍵是開發高速光邏輯門器件。光邏輯門還可以實現全光信號提取、全光地址識別和全光復用/解復用等。因此，在未來的全光高速通信網路和新一代光計算機中將有著巨大的套用潛力。國內外均對此展開了廣泛深入的研究。半導體光放大器以其體積小、易於集成、光譜性能好、工作波長範圍寬、回響時間短以及良好的非線性特性等優點，成為各種全光邏輯門中的主要功能器件。

光邏輯門是實現高速光分組交換、全光地址識別、數據編碼、奇偶校驗、信號再生、光計算和未來高速大容量全光信號處理的關鍵器件，同時，光邏輯門的發展是實現電計算向光計算跨越的橋樑，可以突破“電子瓶頸”的限制，提高網路容量，實現全光3R再生。

實現光學邏輯門的非線性光學原理

半導體光放大器具有良好的非線性，十分適合用於實現光邏輯功能。全光邏輯門的實現主要是基於半導體光放大器中的交叉增益調製波長轉換原理，在忽略放大的自發輻射引起的載流子消耗的條件下，波長的轉換過程可以用以下2個方程描述：

其中，N是有源區中載流子的濃度，I是注入電流，e是電子電量，V是有源區體積，Γ是模場限制因子，A是有源區橫截面積，h是普朗克常數，C是真空中光速，下標S和C分別對應信號光和探測光， 是對應光波的增益係數，v是光波的頻率， 和 分別對應正向和反向傳播的光功率，喻是有源區內部的損耗係數，R(N)是非輻射複合和自發輻射複合引起的載流子消耗。為準確模擬載流子沿半導體光放大器有源區長度方向的分布，可以採用分段模型進行數值模擬。將有源區分為M段，每段載流子濃度均勻，給定入射光功率，就可以求得整個有源區內載流子濃度N和光功率P在空間上的靜態分布，最後採用龍格—庫塔法求出隨時間變化的輸出光功率。

利用半導體光放大器實現光XOR門

利用半導體光放大器(SOA)實現光XOR門

圖1是基於2個SOA實現XOR功能的原理圖。

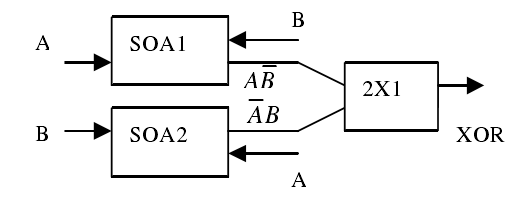
圖1

信號有2束光脈衝分別從左右兩端相向進入SOA，其中，右端的光強遠大於左端的光強，以SOA1為例，當A和B信號都為“1”時，因為SOA1右端有強泵浦光B入射，B將消耗SOA中的絕大部分載流子，由於載流子恢復需要一定時間，因此信號A被飽和吸收，所以SOA1右端可以視為無光脈衝輸出，即輸出為“0”；只有右端無光脈衝輸出時，A才能夠被SOA放大，輸出為“1”，相當於SOA1實現了 運算。同理，下方的SOA2實現了 運算，然後將2路信號通過1個光耦合器耦合到一起輸出，也就是XOR= + ，因此實現了A和B之間的XOR運算。

利用半導體光放大器實現光邏輯與門

本方案是利用級聯的交叉增益調製型波長轉換來實現全光邏輯與門，工作原理為：特定速率的信號光經過摻餌光纖放大器放大後再經耦合器1分為2路，其中一路信號光A和可調諧雷射器提供的連續光（探測光）經耦合器2合路，再經過環行器送入SOA1。2束光在SOA1中可以產生基於交叉增益調製效應的波長轉換現象，信號光攜帶的信息轉換到探測光上，但與原信息反相。第1級SOA1輸出的信號光經環行器輸出，而後經過EDFA2放大，隨後由帶通濾波器1濾出波長轉換後的信號;另一路光信號經過可調諧延時線延時後，和帶通濾波器1輸出的信號一起經過禍合器和環行器耦合進SOA2，適當控制第1級轉換輸出的功率遠大於延時後的信號光功率，因此，當第1級轉換輸出的比特為“1”時，SOA2的增益被抑制，無論信號光為“1”還是“0”，輸出都為“0”；反之，當第1級轉換輸出的比特為“0”信號光為“1”時輸出“1”，為“0”時輸出“0”，因此，經帶通濾波器2(對準信號光波長)濾出的信號就是信號光A和延時後的信號光B的邏輯與運算結果。

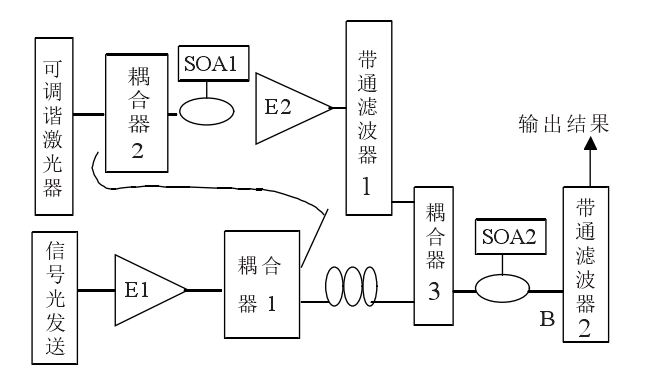
圖2

利用太赫茲光非對稱解復用器

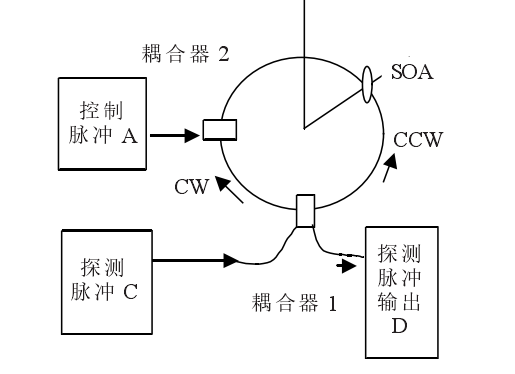
利用太赫茲光非對稱解復用器實現全光邏輯門，此方案原理如圖3所示。

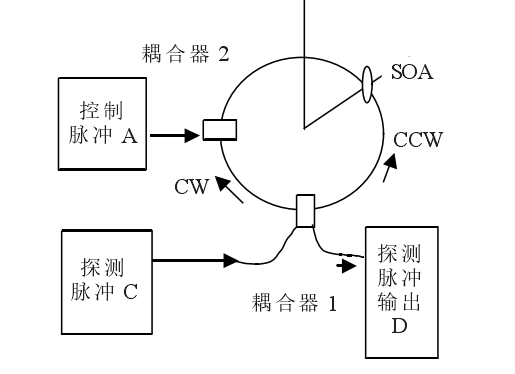
圖3

耦合器1將一段光纖首尾相接，作為非線性元件的SOA非對稱的置於光纖線路中，它偏離環路中心的光程為T/2，控制脈衝經過耦合器2從連線埠A引入環路，探測脈衝從連線埠C注入，控制信號光足夠強，能夠引起SOA中的非線性效應，而探測光很弱，它不在SOA中引起非線性光學效應。此邏輯門的工作過程為:探測光從連線埠C輸入，被耦合器1分為幅度相等的2部分，分別沿順時針(CW)和逆時針(CCW)方向傳輸，在沒有控制光的情況下，CW和CCW光均可獲得SOA的小信號增益，當它們再次回到耦合器1時所獲得的相移也相等，因此，2束光在連線埠D相干相消，而光全部從連線埠C反射；反之，當有控制光從連線埠A輸入，控制光經耦合器2注入環路中，適當調節探測光和控制光之間的時延，使得控制光在CCW之後CW之前到達SOA，這樣，在控制光的作用下，CW將獲得額外的非線性相移，經耦合器1再次禍合後，從連線埠D輸出，相當於實現了探測光與控制光的邏輯與運算。

數字光計算機

數字光計算機通常是指用光學手段實現數字運算所需要的軟體和硬體的通稱，技術上以列陣光學和非線性光學為基礎，構想通用或專用的全光數字計算機。正如電子計算機一樣，數字光計算機也是由最基本的光學邏輯門組成，所不同的是，這種邏輯結合了光學和光學邏輯器件的特性。

數字光計算機中，最常用的基值編碼方法是光強度編碼法。如在二進制光邏輯編碼中，邏輯“1”用高光強編碼，而邏輯“0”則用低光強編碼。這種編碼稱“亮真”邏輯。如果採用相反編碼則稱“暗真”邏輯。

邏輯值也可用各種光學參量表示的空間圖形(或稱空間編碼)進行編碼。這種編碼比較適合光計算機。空間編碼邏輯可充分利用傳統的光學二維處理方法。簡單例子如雙軌編碼，在雙軌編碼中，各數據位被編碼成雙軌陣列，每比特由一對鄰接元表示，兩鄰接單元只有一個單元透光。例如，在“1”比特雙軌碼編碼中，上面單元透光，下面單元則不透光；而在“0”比特雙軌碼錶示中，透光排列次序剛好相反。雙軌碼和亮真(或暗真)邏輯的區別是，雙軌碼中“0”、“1”基值能量相同，而亮真(或暗真)邏輯正是藉助能量不同來實現對不同基值的邏輯編碼。另一個區別是雙軌碼邏輯編碼時單比特表示所需要的空間增加。

光計算機對光學邏輯器件要求有：

（1）對可級聯性，不僅要求在光功率上可級聯，而且在光波上、光束形狀和脈衝形狀方面也要求能實現級聯；

（2）對輸出，應具有增益輸出能力；

（3）對光邏輯級重建，要求功率級，光束或脈衝形狀等都應能重建；

（4）為使得器件在系統中實用化，要求所有器件及其偏置高度均勻，否則需要調整系統中每一器件，而這往往是難以達到的；

（5）對光邏輯器件，輸入輸出還要求隔離良好。對一個三端器件，如三極體由於反饋回三極體的輸出信號沒有被器件本身放大，因此輸入輸出隔離效果比較好；對二端器件，如隧道二極體或光雙穩器件由於對輸入輸出沒有任何隔離，輸出同輸入一樣被放大，因此難以構成比較大的系統；

（6）受激放大器件(如雷射放大器)其反向和正向放大機理相同，對輸入輸出也沒有進行隔離，所以即使在小系統中也需要對輸入輸出進行隔離，以防止反饋引起的級聯誤差；

（7）大多數光學邏輯器件運轉功率都比較大，難以製造成數字系統所要求的大列陣。

幾何光學中的邏輯符號法則

以下是邏輯符號法則：

（1）不加撇的字母表示是物空間的物理量，加撇的字母表示是像空間的物理量。

（2）坐標係為O-yz直角坐標系。坐標原點O位於球面頂點或主點，y-軸正向為由下向上，z-軸正向為由左向右，光軸與z-軸重合。

（3）與距離直接有關的字母表示坐標。對於物點和像點只需標出其z-坐標即可，不需標出物距和像距，因為它們可以由坐標很簡單的求出。

（4）標註的角量全為銳角。入射角和折射角分別以i和i'表示。由於反射角等於入射角，故反射角也用i表示。對於其餘的三個角(入射光線與光軸的夾角、出射光線與光軸的夾角、法線與光軸的夾角)，以光軸為起始邊，順時針旋轉的其角標為正數；逆時針旋轉的其角標為負數，標註時需在其前填一負號以使之變為角度。之所以這樣規定是為了簡化公式的推導。

邏輯符號法則既適用於從左到右的入射光線，也適用於從右到左的入射光線，因為坐標系與光線方向無關。儘管如此，實用上總是使入射光線從左到右行進，故通常情況下默認入射光線從左到右行進。