優美標號

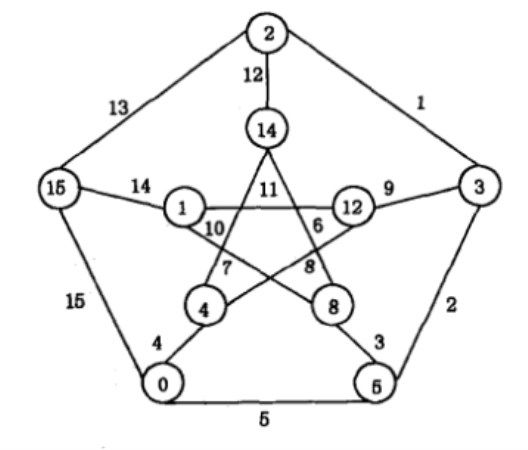
優美標號(graceful labeling)是圖的一種標號，指用非負整數標記圖的頂點的一種方法。用{0，1，2，…，q}中不同的整數標記一個圖的頂點(q為圖的邊數)，並以兩端點標號差的絕對值標記相應的邊，所得邊的標號集若為{1，2，…，q}，則稱這個標號為圖的優美標號，若存在{0，1，2，…，q}中的一個數x，使圖的任一條邊的兩個端點的標號一個比x大，一個不比x大，則稱這個優美標號為交錯標號，若用{0，1，…，q+1-k}中的不同的整數標記圖的頂點且所得邊的標號集為{k，k+1，…，q+k-1}，則稱這個標號為k優美標號，1優美標號就是如上定義的優美標號，存在優美標號的圖稱為優美圖，存在k優美標號的圖稱為k優美圖，邊-優美標號是用正整數標記圖的邊的一種方法，用{1，2，…，q}中不同的整數標記圖的邊，並以所有關聯邊的標號的和模p(p為圖的節點數)標記相應的頂點，若所得頂點標號集為{0，1，…，p-1}，則稱這個標號為邊-優美標號，存在邊-優美標號的圖稱為邊-優美圖，集-優美標號是用集合標記圖的節點的一種方法，2表示有限集X的所有子集組成的集合，用2中的不同元標記圖的頂點，並以兩端點標號的對稱差標記相應的邊，若所得邊的標號互不相同且邊號集為2\{∅}，則稱這個標號為集-優美標號，存在集-優美標號的圖稱為集-優美圖。

基本介紹

• 中文名：優美標號
• 外文名：graceful labeling
• 所屬學科：數學
• 所屬問題：組合學(圖與超圖)
• 簡介：用非負整數標記圖的頂點的方法

基本介紹

優美標號的研究始於20世紀60年代，研究的中心問題是哪些圖是優美圖，至今尚無一般方法來判斷一個圖是否是優美圖，僅知道很少一部分圖是優美圖。

設是p個頂點q條邊的簡單圖。

定義1 設是單射，若g的誘導映射是雙射，，則稱g是G的一個優美標號(graceful labeing)，並稱G是一個優美圖。

圖1

例如圖1給出了彼得森(Petersen)圖的一種優美標號。

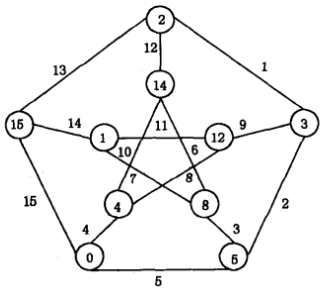
關於優美標號的主要結論

關於優美標號的主要結論：

1．當m，n為偶數或時，是優美的(Jungreis和Reid)。

2．對於任意正整數n≥3，是優美的(梁志和)。這裡是指路P₂上所有距離為2的點之間再連一條邊而得到的圖。

3．蛛網圖是優美的(1980年，Koh)。這裡是指具有同心O的m個圈，從O發出的射線將O與每個上相應的點連線得到的圖。

關於優美標號的主要猜想

關於優美標號的主要猜想：

1) 所有的樹是優美的(1963年，Ringel和Kotzig)，其子猜想是：所有的龍蝦樹(樹去掉1度點後成的毛毛蟲)是優美的(1979年，Bermord)。(尋找不優美的樹至今未果)。

2)優美的充要條件是，(Frucht和Salinas)．

3) 當或時，n塊三角仙人掌是優美的(Rosa)，這裡三角仙人掌是指所有塊皆為三角形的連通圖。

4) 對自然數m，n，圖和是優美的(1984年，Kotzig)，這裡是m個圈的不交並。

5)1983年Lee猜想：對任意n>1和圖G的頂點集上置換f，f-置換圖是優美的。(這裡P_n是有n個點的路，f-置換圖是指：若G₁和G₂是G的2個不交的拷貝，f是G的頂點集S(n)上置換，將G₁中的每個點j與G₂中點連邊而得到的圖，記為。1994年Lee等進一步猜想：若G是具有n個點的優美圖，但不是二分圖，則對S(n)上任意置換f，是優美的。

對上述猜想目前均未獲徹底解決，已經知道的主要結果有：

1)路P_n和星形圖是優美的；毛毛蟲(樹去掉1度點後形成的一條路或平凡圖)是優美的；具有至多27個點的樹是優美的等等。一些由較小優美樹構造較大優美樹的方法。

2)優美性已經解決；當

和時，是優美的。

3)已經證明對於荷蘭風車圖(m個三角形恰有一個公共點的圖)，三角蛇(即塊割點圖為一條路的三角仙人掌)，當或時是優美圖。

4)康慶德等人證明了對所有n≥3都是優美的。

5)優美的必要條件是或；k≥1時是優美的；m≥2時均是不優美的；還有更進一步的結果：不但具有優美標號，而且還具有更強的標號——平衡標號。

6)已知優美置換圖有：當G是星形圖，圈C_n或路P_n，f是恆等置換時；以及是任意置換時等。