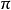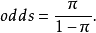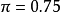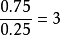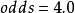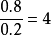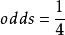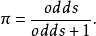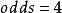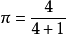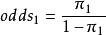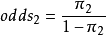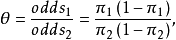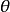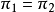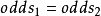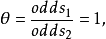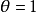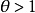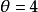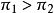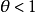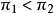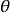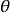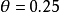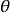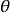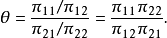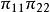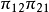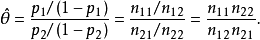優勢比(odds ratio；OR)是另外一種描述機率的方式。優勢比將會告訴我們某種推測的機率比其反向推測的機率大多少。換句話說，優勢比是指某種推測為真的機率與某種推測為假的機率的比值。比如下雨的機率為0.25，不下雨的機率為0.75。0.25與0.75的比值可以約分為1比3。因此，我們可以說今天將會下雨的優勢比為1:3(或者今天不會下雨的機率比為3:1)。
通常情況下，人們習慣於通過與某一主張相反的優勢比的方式進行表達，例如，對於“寶馬Phar Lap將會在德比賽馬中最終勝出”這一主張，人們習慣於使用賠率(即Phar Lap會輸的機率比)。然而，科學家們卻習慣於使用支持某一主張的優勢比。如果我們認為反對兩個血樣匹配的優勢比為1 000 000:1，那么科學家們習慣於使用支持這一主張的優勢比1:1 000 000。可以使用下面的公式，將優勢比a:b轉換為機率：P=a/(a+b)，其中，a是指支持某一主張的機率，b是指反對某一主張的機率。在上述下雨的例子中，支持下雨的優勢比為1:3。因此，a=1，b=3，下雨的機率=1/(1+3)=1/4=0.25。
基本介紹
- 中文名：優勢比、比數比
- 外文名：odds ratio；OR
- 別名：比值比，交叉乘積比
- 所屬學科：數學（統計學）
- 相關概念：優勢，列聯表，相對風險等
基本介紹,列聯表,優勢的概念,優勢比的定義,優勢比的性質,
基本介紹
列聯表
列聯表(contingency table)是按兩種屬性分類的一種統計表，用來說明兩種屬性之間的關係。一種屬性分類為行，另一種屬性分類為列。通過列聯表可觀察兩種屬性因素之間的相互聯繫，常用的統計列聯表有2×2、2×3、3×3等形式。
列聯表是將樣本觀測數據按兩個或更多定性屬性分類時所列出的頻數表。例如，對隨機抽取的1000人按性別(男或女)及色覺(正常或色盲)兩個屬性分類得到兩行兩列的列聯表 (見表1)。一般地，若總體中的每個個體可按屬性A與B分類，A、B分別有r與c個水平，則按樣本中屬於不同水平組合的頻數可以排成r行c列的二維列聯表，若考慮的屬性多於兩個，也可按類似的方法作出多維列聯表。
男 | 女 | 合計 | |
正常 | 442 | 514 | 956 |
色盲 | 38 | 6 | 44 |
合計 | 480 | 520 | 1000 |
優勢的概念
下面介紹2×2列聯表關聯性的一種度量-優勢比(odds ratio)，它是針對屬性數據的最重要模型中的參數。
對於成功的機率
，成功的優勢(odds)定義為
優勢是一個非負實數，當它大於1時成功比失敗的機率大。當優勢為
時，成功的可能性是失敗的4倍。當成功的機率是0.8時，失敗的機率為0.2，則成功的優勢為
，於是我們預期每出現1次失敗會有4次成功。當
，失敗的可能性是成功的4倍，我們預期每出現4次失敗會有1次成功。
成功的機率是優勢的函式，
優勢比的定義
在2×2表中，第1行成功的優勢為
，第2行成功的優勢為
。兩行的優勢的比值，
優勢比的性質
優勢比可以等於任何的非負實數。當X和Y獨立，
時，
，從而
獨立值
是兩組比較的基準。當優勢比處於1的兩側，它分別代表了不同類型的關聯性。當
時，第1行中“成功”的優勢比第2行大。例如，當
時，第1行中“成功’’的優勢是第2行“成功”的優勢的4倍。那么，第1行的試驗比第2行的試驗更容易成功；即
。當
時，第1行試驗比第2行的試驗更不容易成功：即
。
當一個值是另一個值的倒數時，它們具有相同的關聯程度，只是方向相反。例如，當
時，第1行成功的優勢是第2行成功優勢的0.25倍。換句話說，第2行成功的優勢是第1行成功的優勢的1/0.25=4.0倍。當行或列類別的排列順序交換以後，新的值是原值的倒數。行或列類別的排列順序通常是任意的，所以不論我們得到的優勢比是4.0還是0.25，這僅僅與行和列中各類別是如何排列的有關。
當原表的行和列顛倒後，優勢比並不改變，所以表的行可以作為列，列可以作為行，不論我們是把列當作回響變數而把行當作解釋變數，還是把列當作解釋變數而把行當作回響變數，我們都會得到相同的優勢比。所以我們在估計時並不需要去設定某個變數為回響變數，相反的，相對風險需要我們設定回響變數，它的值還依賴於我們是把第一個還是第二個結果類別當作成功。
當兩個變數均是回響變數，優勢比能由聯合機率決定
樣本優勢比等於各行樣本優勢的比，
