傳播子是指量子場論中,場的運動方程的格林函式。傳播子用於描述場論中單粒子運動的基本工具,常常等於兩個場的編時乘積。
基本介紹
- 中文名:傳播子
- 外文名:propagator
- 理論:量子場論
- 作用:描述場論中單粒子運動的基本工具
- 傳播子方程:有源的Klein-Gorden方程
- 套用學科:物理
概念
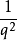

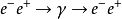
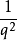

 圖1
圖1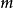

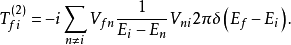
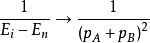
基本原理
 圖2
圖2
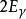
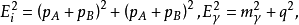
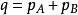

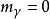


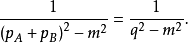
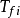

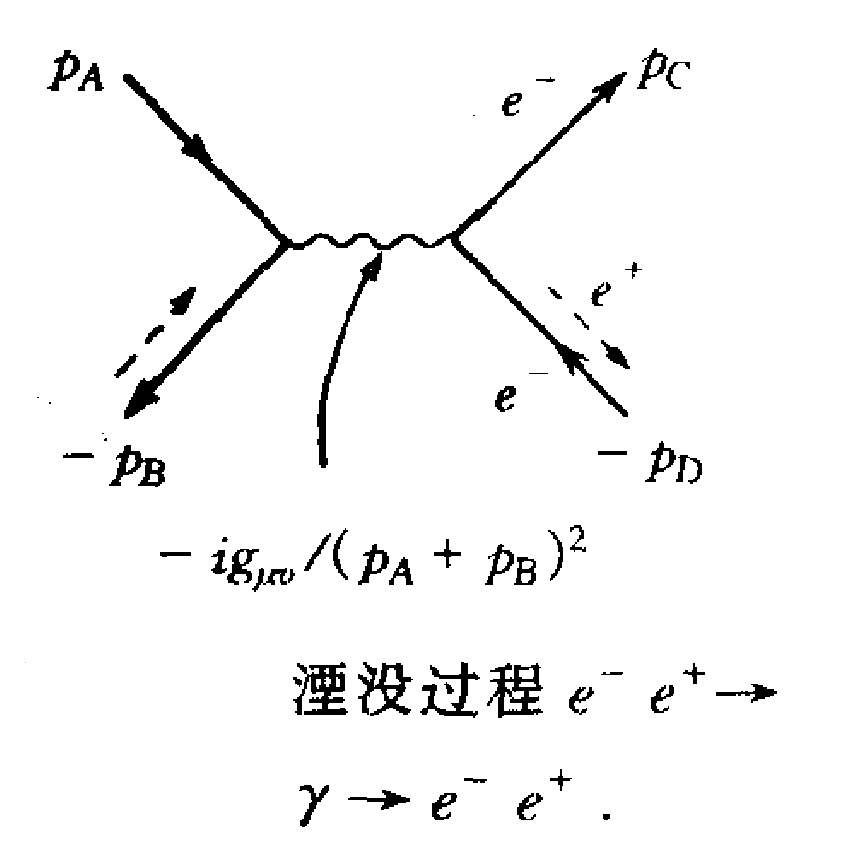
傳播子是指量子場論中,場的運動方程的格林函式。傳播子用於描述場論中單粒子運動的基本工具,常常等於兩個場的編時乘積。
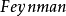
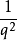

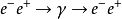
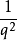

 圖1
圖1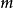

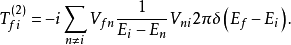
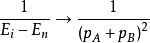
 圖2
圖2
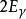
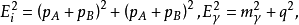
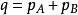

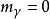


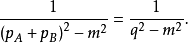
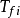

傳播子是指量子場論中,場的運動方程的格林函式。傳播子用於描述場論中單粒子運動的基本工具,常常等於兩個場的編時乘積。...
費曼傳播子量子電動力學 編輯 在粒子物理學中,量子電動力學(英語:Quantum Electrodynamics,簡稱QED)是電動力學的相對論性量子場論。它在本質上描述了光與物質間的...
傳播子也屬於基本粒子。傳遞強作用的膠子共有8種,1979年在三噴注現象中被間接發現,它們可以組成膠子球,由於色禁閉現象,至今無法直接觀測到。光子傳遞電磁相互作用...
帶電粒子之間電磁相互作用的傳播子是質量為零、自旋為1的光子。 原來有學者認為,核子之間的強相互作用(核力)是靠π介子傳遞的,但由於核子和π介子都是由夸克組成...
粒子2到2散射過程,在量子場論中計算其費曼圖時,考慮到交叉對稱性,按照傳播子的四動量對樹圖進行分類;當傳播子的四動量是Mandelstam變數中的s時,我們稱這類圖為s...
在此機制中,希格斯場引起自發對稱性破缺,並將質量予規範傳播子和費米子。希格斯粒子是希格斯場的場量子化激發,它通過自相互作用而獲得質量。 2013年3月,歐洲核子...
物理上,特別是量子場論中,物理系統的滿足經典運動方程的位形稱為在殼的,而其它的則稱為離殼的。費曼圖中和內部傳播子相關的虛擬粒子通常允許離殼,但該進程的...
三.規範玻色子(規範傳播子) (14種) 49.引力型-中性膠子(Ⅰ型開弦) 上夸克-上夸克 50.引力型-中性膠子(Ⅰ型開弦) 反上夸克-反上夸克 51.磁力型-中性膠...
粒子2到2散射過程,在量子場論中計算其費曼圖時,考慮到交叉對稱性,按照傳播子的四動量對樹圖進行分類;當傳播子的四動量是Mandelstam變數中的u時,我們稱這類圖為u...
粒子2到2散射過程,在量子場論中計算其費曼圖時,考慮到交叉對稱性,按照傳播子的四動量對樹圖進行分類;當傳播子的四動量是Mandelstam變數中的t時,我們稱這類圖為t...
三、規範玻色子(規範傳播子) (14種) 49、引力型-中性膠子(Ⅰ型開弦) 上夸克-上夸克 50、引力型-中性膠子(Ⅰ型開弦) 反上夸克-反上夸克 51、磁力型-中...
“源一流一用”基本原理,構造出農業信息生產子系統、傳播子系統和施效子系統;接著探討了農業信息服務系統的動力機制和運行模式,通過比較分析得出:“政府主導、聯合...
新聞本體理論與環境理論是對新聞信息傳播系統本體的研究構成了新聞本體理論;對新聞信息傳播系統與環境系統的關係的研究構成新聞系統環境理論。把社會信息傳播作為一個大...
2、切斷傳播途徑革除食用人體組織陋習,不食用朊毒體病動物肉類及製品,不以動物組織飼料餵養動物,醫療操作嚴格遵守消毒程式,提倡使用一次性神經外科器械。...
4.5諧振子系統 4.5.1諧振子內容回顧 4.5.2諧振子系統的傳播子 4.5.3用傳播子方法解諧振子問題 第5章散射理論 5.1基本問題 5.1.1兩粒子的散射 5...
