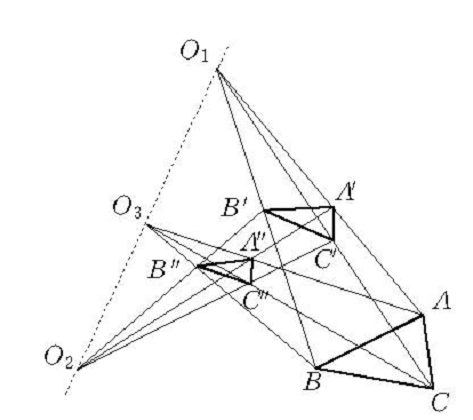
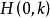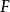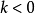位似軸(homothetic axis)亦稱相似軸,指與三個位似圖形有關的一條直線,是平面上或空間中的三個互相位似的圖形的三個位似中心所在的同一條直線。位似軸上外位似中心的個數一定是奇數,即或是一個或是三個。
基本介紹
- 中文名:位似軸
- 外文名:homothetic axis
- 別稱:相似軸
- 所屬學科:數學
- 所屬問題:平面幾何(比例與相似形)
- 相關概念:位似圖形,位似變換,位似中心等
基本介紹,相關介紹,位似變換,位似圖形,
基本介紹
位似圖形有下列性質:
1. 位似圖形一定是相似圖形,並且位似圖形的對應線段平行,過對應頂點的直線共點。
2. 如果三個圖形兩兩位似,那么每兩個位似圖形的位似中心(共三個)一定共線,這條直線叫做這三個圖形的位似軸(如圖1)。
3. 平面上任意兩個不等的圓可以看成是一對位似圖形,並且有兩種方法使它們位似,其中,兩圓心是一對對應點。
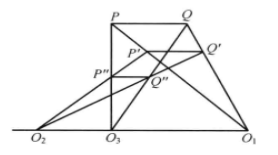 圖1
圖1相關介紹
位似變換
定義1 是平面
是平面 上一定點,H是平面上的變換,若對於任一對對應點
上一定點,H是平面上的變換,若對於任一對對應點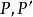 ,都有
,都有 (k為非零實數),則稱H為位似變換,記為
(k為非零實數),則稱H為位似變換,記為 ,
, 叫做位似中心,k叫做位似比。
叫做位似中心,k叫做位似比。


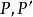



定義中的條件“ ”等價於如下三個條件:
”等價於如下三個條件:

(1) 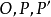 三點共線;
三點共線;
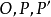
(2) ;
;

(3) 當 時,點
時,點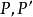 在點
在點 同側(此時
同側(此時 叫做外位似中心);當
叫做外位似中心);當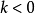 時,點
時,點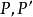 在點
在點 異側(此時點
異側(此時點 叫做內位似中心)。
叫做內位似中心)。

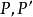


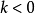
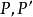


顯然,位似變換 就是恆等變換,而位似變換
就是恆等變換,而位似變換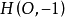 是以點
是以點 為中心的中心對稱變換。
為中心的中心對稱變換。

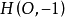

位似變換由位似中心與位似比所確定,也可以由一對對應點和位似中心(或位似比)確定,此外,我們還有下述判定定理:
定理1 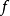 是平面上一個變換,那么
是平面上一個變換,那么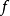 是位似變換或平移變換的充分必要條件是,對於
是位似變換或平移變換的充分必要條件是,對於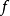 的任兩對對應點
的任兩對對應點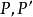 和
和 ,總有
,總有
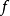
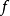
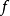
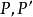


此定理給出了判別位似變換的又一標準,平移是位似變換的一種極端情況,它的位似中心是無窮遠點,位似比等於1。
位似變換具有下列性質:
1.位似變換是相似變換,所以位似變換具有相似變換的所有性質。
2.具有相同位似中心的所有位似變換構成一個變換群。
3.在位似變換下,位似中心是不變點,過位似中心的直線是不變直線。
4.在位似變換下,對應線段之比相等,對應角相等且轉向相同,不過中心的對應直線平行(當 時,同向平行;當
時,同向平行;當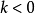 時,反向平行)。
時,反向平行)。

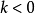
5.兩個不同中心的位似變換的乘積或者是位似變換(此時三個位似中心共線);或者是平移變換(平移方向平行於兩中心所在直線)。
位似圖形
定義2 是兩個平面圖形,如果存在一個位似變換
是兩個平面圖形,如果存在一個位似變換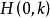 ,使得
,使得