位似法作圖

利用位似變換的性質解作圖題的方法，叫做位似法，位似法作圖，常先捨棄圖形的大小、位置條件（或部分位置條件），作出滿足形狀要求的圖形F'，然後選擇適當的位似中心和位似比，作出符合大小要求（或位置要求），並與F'位似的圖形F。

基本介紹

• 中文名：位似法作圖
• 外文名：construction with homothetic method
• 所屬學科：數學
• 所屬問題：平面幾何(尺規作圖)
• 簡介：利用位似變換的性質作圖

基本介紹

位似法作圖(construction with homothetic method)是一種常用的作圖方法，利用位似變換的方法作圖。要作出滿足某些條件的圖形，可以先放棄一兩個條件，作出與其位似的圖形，然後利用位似變換，將這個與其相似的圖形放大或縮小，以滿足全部條件，從而作出所要求作的圖形。例如，要求作銳角三角形ABC的內接正方形DEFG，先放棄一個頂點F在邊AC上的條件，作出與正方形DEFG位似的正方形D′E′F′G′(如圖1)，然後利用位似變換將正方形D′E′F′G′放大，以滿足全部條件，從而求得所要作的正方形DEFG。

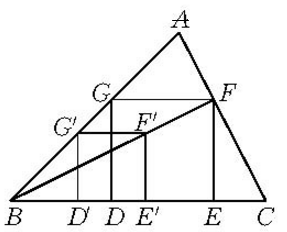
圖1

例題解析

【例1】在已知半圓內求作內接矩形，使矩形的一邊在半圓直徑上，並且相鄰邊之比等於定比。

已知 以AB為直徑的半圓O，線段m,n。

求作 矩形EFGH，使EF在AB上，點G，H在圓弧上，並且

分析 因為“矩形鄰邊之比為定比m:n”這一條件決定了矩形的形狀，而內接於半圓的位置條件決定了矩形的大小，於是先作出符合形狀要求的矩形E'F'G'H'，然後以圓心O為位似中心，作出與E'F'G'H'位似的內接於半圓的矩形。

作法 (1)以O為中點，在AB上作線段E'F'，使E'F'=m。

(2)以E'F’為一邊，作矩形E'F'G'H'，使F'G'=n(如圖2)。

(3)連OG'，OH'，設交半圓於點G，H。

(4)連GH，過點G，H作AB的垂線，垂足分別是F，E。

則EFGH為所求作的矩形。

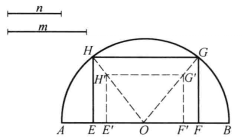
圖2

證明 略。

討論 本題恆有一解.

【例2】已知三角形的兩內角以及兩角夾邊與高的和，求作三角形。

已知 角a,β，線段l。

求作 △ABC，使∠A=a，∠B=β，高CD與AB的和為l。

分析 ∠A=a，∠B=β 是△ABC的形狀條件，CD+AB=l是決定△ABC大小的條件。

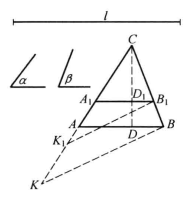
圖3

先作出符合形狀要求的圖形△CA₁B₁，使∠A₁=α，∠B₁=β，以點C為位似中心作△CA₁B₁的位似△ABC，下面決定位似比。

因為

所以

則

即

這樣，點B可確定，點A亦隨之可定。

作法 (1)作△A₁B₁C，使∠A₁=α，∠B₁=β，再作A₁B邊上的高CD₁(如圖3)。

(2)在射線CA₁上取CK₁=CD₁+ A₁B₁，取CK=l。

(3)連K₁B₁，過點K作K₁B₁的平行線交CB₁於點B。

(4)過點B作A₁B₁的平行線交CA₁於點A。

則△ABC為所求。